题目内容
18.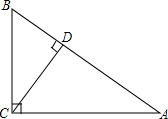 △ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.
△ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.解:如图,作CD⊥AB,垂足为D,△ABC把BC看作底,则AC是高,此时面积为$\frac{1}{2}$BC•AC;若把AB看作底,则CD是高,此时面积为$\frac{1}{2}$AB•CD.
∴$\frac{1}{2}$×6×8=$\frac{1}{2}×10•CD$.
∴CD=$\frac{24}{5}$.
分析 由等量代换可得到∠B+∠BCD=90°,故△BDC是直角三角形,即CD⊥AB,再由面积法可求得CD的长.
解答 解:如图,作CD⊥AB,垂足为D,△ABC把BC看作底,则AC是高,此时面积为$\frac{1}{2}$BC•AC;若把AB看作底,则CD是高,此时面积为$\frac{1}{2}$AB•CD.
∴$\frac{1}{2}×6×8$=$\frac{1}{2}×10•CD$.
∴CD=$\frac{24}{5}$.
故答案为:$\frac{1}{2}$BC•AC,$\frac{1}{2}$AB•CD,$\frac{1}{2}×6×8$,$\frac{1}{2}×10•CD$,$\frac{24}{5}$.
点评 本题考查了利用直角三角形的判定和利用面积法求直角三角形的斜边上的高的长.

练习册系列答案
相关题目
3.若ab≠1,且a2+2015a+9=0,9b2+2015b+5=0,则$\frac{a}{b}$的值是( )
| A. | $\frac{9}{5}$ | B. | $\frac{5}{9}$ | C. | -$\frac{2015}{5}$ | D. | -$\frac{2015}{9}$ |