题目内容
8.用适当的方法解下列方程:(1)2(x+3)2=8;
(2)4x2-4$\sqrt{2}$x+1=0;
(3)2x2-5x=0.
分析 (1)直接利用直接开平方法解方程得出即可;
(2)利用公式法解方程得出即可;
(3)利用因式分解法解方程得出即可.
解答 解:(1)2(x+3)2=8
(x+3)2=4,
解得:x1=-1,x2=-5;
(2)4x2-4$\sqrt{2}$x+1=0
△=b2-4ac=32-16=16,
则x=$\frac{4\sqrt{2}±\sqrt{16}}{8}$,
解得:x1=$\frac{\sqrt{2}+1}{2}$,x2=$\frac{\sqrt{2}-1}{2}$;
(3)2x2-5x=0
x(2x-5)=0,
解得:x1=0,x2=2.5.
点评 此题主要考查了直接开平方法以及公式法和因式分解法解方程,正确应用公式法解方程是解题关键.

练习册系列答案
相关题目
17.方程x2+x=12的根为( )
| A. | 4或3 | B. | -4或-3 | C. | -3或4 | D. | -4或3 |
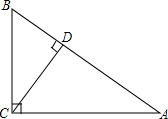 △ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.
△ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长. 如图,A、B、C三点在数轴上,点C在点A与点B之间,且AC:BC=1:5
如图,A、B、C三点在数轴上,点C在点A与点B之间,且AC:BC=1:5