题目内容
3.若ab≠1,且a2+2015a+9=0,9b2+2015b+5=0,则$\frac{a}{b}$的值是( )| A. | $\frac{9}{5}$ | B. | $\frac{5}{9}$ | C. | -$\frac{2015}{5}$ | D. | -$\frac{2015}{9}$ |
分析 把9b2+2015b+5=0变形为5•($\frac{1}{b}$)2+2015•$\frac{1}{b}$+9=0,则a和$\frac{1}{b}$可看作方程5x2+2015x+9=0的两根,然后根据根与系数的关系求解.
解答 解:∵5a2+2015a+9=0,9b2+2015b+5=0,
∴5a2+2015a+9=0,5•($\frac{1}{b}$)2+2015•$\frac{1}{b}$+9=0,
∵ab≠1,即a≠$\frac{1}{b}$,
∴a和$\frac{1}{b}$可看作方程5x2+2015x+9=0的两根,
∴a•$\frac{1}{b}$=$\frac{9}{5}$.
故选:A.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列说法中,正确的是( )
| A. | -a的绝对值等于a | |
| B. | 一个数的绝对值是它的相反数,则这个数一定是负数 | |
| C. | 若两个有理数的绝对值相等,则这两个数互为相反数 | |
| D. | 一个有理数的绝对值不小于它自身 |
15.下列各式正确的是( )
| A. | $\sqrt{1\frac{9}{16}}$=$\frac{5}{4}$ | B. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | C. | $\sqrt{0.25}$=0.05 | D. | -$\sqrt{-49}$-(-7)=7 |
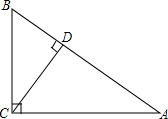 △ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.
△ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.