题目内容
7.用公式法解下列方程:(1)x2-2x-8=0 (2)x2+2x-4=0
(3)2x2-3x+2=0 (4)3x(3x-2)+1=0
(5)$\frac{3}{2}$x2-$\frac{1}{2}$x-1=0 (6)x2-2$\sqrt{2}$x+2=0.
分析 各方程整理为一般形式,找出a,b,c的值,代入求根公式即可求出解.
解答 解:(1)这里a=1,b=-2,c=-8,
∵△=4+32=36,
∴x=$\frac{2±6}{2}$,
解得:x1=4,x2=-2;
(2)这里a=1,b=2,c=-4,
∵△=4+16=20,
∴x=$\frac{-2±2\sqrt{5}}{2}$=-1±$\sqrt{5}$;
(3)这里a=2,b=-3,c=2,
∵△=9-16<0,
∴此方程无解;
(4)方程整理得:9x2-6x+1=0,
这里a=9,b=-6,c=1,
∵△=36-36=0,
∴x=$\frac{2±6}{2}$,
∴此方程解为x1=x2=$\frac{1}{3}$;
(5)方程整理得:3x2-x-2=0,
这里a=3,b=-1,c=-2,
∵△=1+24=25,
∴x=$\frac{1±5}{6}$,
解得:x1=1,x2=-$\frac{2}{3}$;
(6)这里a=1,b=-2$\sqrt{2}$,c=2,
∵△=8+8=16,
∴x=$\frac{2\sqrt{2}±4}{2}$=$\sqrt{2}$±2,
解得:x1=$\sqrt{2}$+2,x2=$\sqrt{2}$-2.
点评 此题考查了解一元二次方程-公式法,熟练掌握求根公式是解本题的关键.

练习册系列答案
相关题目
15.下列各式正确的是( )
| A. | $\sqrt{1\frac{9}{16}}$=$\frac{5}{4}$ | B. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | C. | $\sqrt{0.25}$=0.05 | D. | -$\sqrt{-49}$-(-7)=7 |
17.方程x2+x=12的根为( )
| A. | 4或3 | B. | -4或-3 | C. | -3或4 | D. | -4或3 |
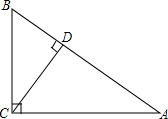 △ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.
△ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.