题目内容
18.计算:1+$\frac{1}{1+2}+\frac{1}{1+2+3}+…+\frac{1}{1+2+3+…+2015}$.分析 利用n个连续自然数的和为$\frac{1}{2}$n(n+1),进一步利用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$拆分抵消得出答案即可.
解答 解:原式=2×($\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$)
=2×($\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$)
=2×(1-$\frac{1}{2016}$)
=2×$\frac{2015}{2016}$
=$\frac{2015}{1008}$.
点评 此题考查有理数的混合运算,掌握连续自然数的和的计算公式和分数的拆分规律是解决问题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
3.下列说法中,正确的是( )
| A. | -a的绝对值等于a | |
| B. | 一个数的绝对值是它的相反数,则这个数一定是负数 | |
| C. | 若两个有理数的绝对值相等,则这两个数互为相反数 | |
| D. | 一个有理数的绝对值不小于它自身 |
 有理数a、b在数轴上的位置如图所示.
有理数a、b在数轴上的位置如图所示.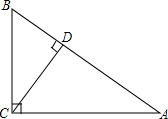 △ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.
△ABC中,∠C=90°,BC=6,AC=8,AB=10,求边AB上的高的长.