题目内容
17.已知⊙O的半径为1,点P到圆心的距离为m,且关于x的一元二次方程x2-2x+m=0有两个不相等实数根,则点P与⊙O位置关系是点P在圆内.分析 关于x的方程x2-2x+m=0有两个不相等的实数根,即判别式△=b2-4ac>0.即可得到关于m的不等式,从而求得m的范围,进而判断点P与⊙O的位置关系.
解答 解:∵a=1,b=-2,c=m,
∴△=b2-4ac=(-2)2-4×1×m=4-4m>0,
解得:m<1.
则点P在⊙O内部.
故答案为:点P在圆内.
点评 本题考查了点与圆的位置关系,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
7.为测量某特种车辆的性能,研究制定了行驶指数P,P=K+1000,而K的大小与平均速度v(km/h)和行驶路程s(km)有关(不考虑其他因素),K由两部分的和组成,一部分与v2成正比,另一部分与sv成正比.在实验中得到了表格中的数据:
(1)用含v和s的式子表示P;
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
| 速度v | 40 | 60 |
| 路程s | 40 | 70 |
| 指数P | 1000 | 1600 |
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
8.下列说法错误的是( )
| A. | 直径是圆中最长的弦 | B. | 半径相等的两个半圆是等弧 | ||
| C. | 面积相等的两个圆是等圆 | D. | 长度相等的两条弧是等弧 |
 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,1),点D的坐标为(6,-1).
如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,1),点D的坐标为(6,-1).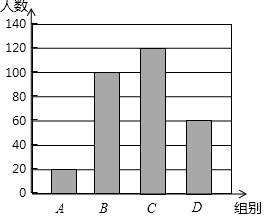 国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.根据上述信息解答下列问题:
国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.根据上述信息解答下列问题: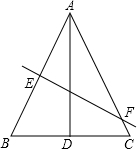 如图,△ABC中,AB=AC,BC=5,S△ABC=15,AD⊥BC与点D,EF垂直平分AB,交AC于F,在EF上确定一点P使PB+PD最小,则这个最小值为( )
如图,△ABC中,AB=AC,BC=5,S△ABC=15,AD⊥BC与点D,EF垂直平分AB,交AC于F,在EF上确定一点P使PB+PD最小,则这个最小值为( )