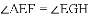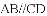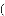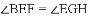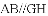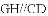题目内容
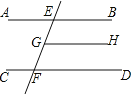
我们定义:如图1,在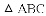
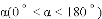 得到
得到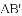
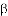
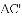
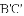
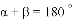 时,我们称
时,我们称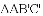
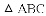
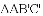
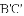
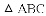
特例感知:
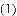
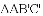
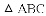
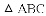

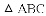
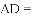
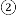
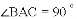 ,
,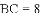
猜想论证:
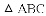
拓展应用
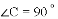 ,
,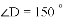 ,
,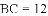
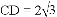 ,
,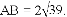 在四边形内部是否存在点P,使
在四边形内部是否存在点P,使
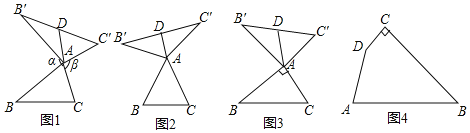
练习册系列答案
相关题目


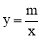 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.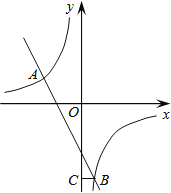
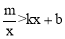 的解集.
的解集.

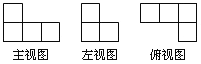
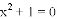 B.
B. 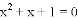 C.
C. 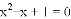 D.
D. 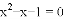







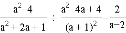 =____.
=____.