题目内容
12.(1)解分式方程:$\frac{8}{4-{x}^{2}}$=$\frac{2}{2-x}$(2)已知$\frac{1}{x}$-$\frac{1}{y}$=3,求代数$\frac{2x-14xy-2y}{x-2xy-y}$的值.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)已知等式左边通分并利用同分母分式的减法法则计算,整理得到x-y=-3xy,代入原式计算即可得到结果.
解答 解:(1)去分母得:8=2(2+x),
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)∵$\frac{1}{x}$-$\frac{1}{y}$=$\frac{y-x}{xy}$=3,即x-y=-3xy,
∴原式=$\frac{2(x-y)-14xy}{x-y-2xy}$=$\frac{-6xy-14xy}{-3xy-2xy}$=4.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20. 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )
 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )| A. | (2,1) | B. | (2,2) | C. | (3,1) | D. | (3,2) |
4.某种细胞开始分裂时有两个,1小时后分裂成4个并死去一个,2小时后分裂成6个并死去一个,3小时后分裂成10并死去一个,按此规律,10小时后细胞存活的个数是( )
| A. | 1023 | B. | 1024 | C. | 1025 | D. | 1026 |
1.一个三角形两边长分别为13cm、15cm,则第三边长可以( )
| A. | 2cm | B. | 11cm | C. | 28cm | D. | 30cm |
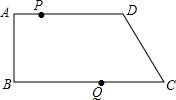 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.