题目内容
4.已知抛物线y=x2+2x-1与x轴的一个交点的坐标为(m,0),则代数式m2+2m-2016的值为( )| A. | 2015 | B. | -2017 | C. | -2016 | D. | -2015 |
分析 直接利用抛物线上点的坐标性质得出关于m的等式,进而得出答案.
解答 解:∵抛物线y=x2+2x-1与x轴的一个交点的坐标为(m,0),
∴0=m2+2m-1,
则m2+2m=1,
故m2+2m-2016=1-2016=-2015.
故选:D.
点评 此题主要考查了抛物线与x轴的交点,正确得出关于m的等式是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.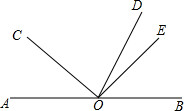 如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=36°,求∠DOE的度数;
(2)若∠AOC=α,则∠DOE=$\frac{1}{2}$α.(用含α的代数式表示)
 如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.(1)若∠AOC=36°,求∠DOE的度数;
(2)若∠AOC=α,则∠DOE=$\frac{1}{2}$α.(用含α的代数式表示)
12.把一条弯曲的河道改成直道,可以缩短航程,其中的道理可以解释为( )
| A. | 线段有两个端点 | B. | 两点之间,直线最短 | ||
| C. | 两点之间,线段最短 | D. | 线段可以比较大小 |
9.下列计算正确的是( )
| A. | 23=6 | B. | -4-16=-20 | C. | -8-8=0 | D. | -5-2=-3 |
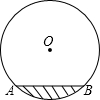 如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,
如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m, 已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.