题目内容
15.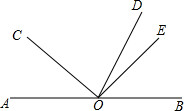 如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.(1)若∠AOC=36°,求∠DOE的度数;
(2)若∠AOC=α,则∠DOE=$\frac{1}{2}$α.(用含α的代数式表示)
分析 (1)先由邻补角定义求出∠BOC=180°-∠AOC=140°,再根据角平分线定义得到∠COD=$\frac{1}{2}$∠BOC=70°,那么∠DOE=∠COE-∠COD=20°;
(2)先由邻补角定义求出∠BOC=180°-∠AOC=140°,再根据角平分线定义得到∠COD=$\frac{1}{2}$∠BOC,于是得到结论.
解答 解:(1)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=36°,
∴∠BOC=144°,
∵OD平分∠BOC,
∴∠COD=$\frac{1}{2}$∠BOC=72°,
∵∠DOE=∠COE-∠COD,∠COE=90°,∴∠DOE=18°;
(2)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=α,
∴∠BOC=180°-α,
∵OD平分∠BOC,
∴∠COD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∵∠DOE=∠COE-∠COD,∠COE=90°,
∴∠DOE=90°-(90°-$\frac{1}{2}$α)=$\frac{1}{2}$α.
故答案为:$\frac{1}{2}$α.
点评 本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
10.对于“0”的说法:①0℃是一个确定的温度;②0为正数;③0不是负数;④0为自然数.正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.已知抛物线y=x2+2x-1与x轴的一个交点的坐标为(m,0),则代数式m2+2m-2016的值为( )
| A. | 2015 | B. | -2017 | C. | -2016 | D. | -2015 |
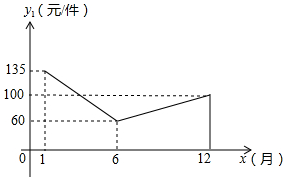 某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.
某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.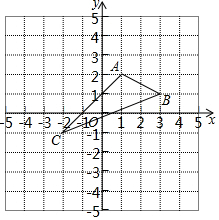 如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).