题目内容
14.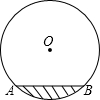 如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,
如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,(1)求排水管内水的深度.
(2)当水面的宽AB为0.8m时,此时水面上升了多少米?
分析 (1)作半径OC⊥AB,连接OA,则CD即为弓形高.根据垂径定理的AD=$\frac{1}{2}$AB,然后根据已知条件求出CD的长;当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P,由此可得OP=0.3,即可得出结果;
(2)根据MN与AB在圆心同侧或异侧时两种情况解答.
解答 解:(1)作半径OC⊥AB,垂足为点D,连接OA,则CD即为弓形高,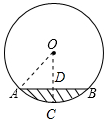
∵OC⊥AB,
∴AD=$\frac{1}{2}$AB,
∵AO=0.5,AB=0.6,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×0.6=0.3,
∴OD=$\sqrt{A{O}^{2}-A{D}^{2}}$=0.4,
∴CD=OC-OD=0.5-0.4=0.1米,即此时的水深为0.1米
(2)当水位上升到水面宽MN为0.8米时,直线OC与MN相交于点P
同理可得OP=0.3,
当MN与AB在圆心同侧时,水面上升的高度为0.1米;
当MN与AB在圆心异侧时,水面上升的高度为0.7米.
点评 本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.下列计算正确的是( )
| A. | (-2ab2)3=-2a3b6 | B. | b3•b3=b6 | C. | a3÷a=2a | D. | (a5)2=a7 |
4.已知抛物线y=x2+2x-1与x轴的一个交点的坐标为(m,0),则代数式m2+2m-2016的值为( )
| A. | 2015 | B. | -2017 | C. | -2016 | D. | -2015 |
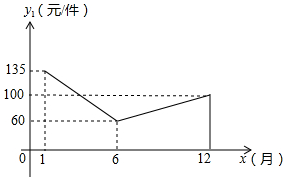 某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.
某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.