题目内容
3.计算:(1)3$\sqrt{3}$-$\sqrt{8}$+$\sqrt{2}$-$\sqrt{27}$
(2)($\sqrt{\frac{1}{2}}$-$\sqrt{\frac{1}{3}}$)-($\sqrt{4.5}$-$\sqrt{0.75}$)
分析 先将各二次根式化简为最简二次根式,然后再合并同类项二次根式即可.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$=-$\sqrt{2}$;
(2)原式=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{3}$-($\sqrt{\frac{9}{2}}$-$\sqrt{\frac{3}{4}}$)=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{3}$-$\frac{3\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$=-$\sqrt{2}$+$\frac{\sqrt{3}}{6}$.
点评 本题主要考查的是二次根式的加减,将各二次根式化简为最简二次根式是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.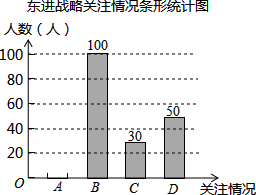 为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
(1)根据上述统计图可得此次采访的人数为200人,M=20,N=0.15;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名汕头市民中,高度关注创建文明城市的汕头市民约有1500人.
 为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | M | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | N |
| D.不知道 | 50 | 0.25 |
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名汕头市民中,高度关注创建文明城市的汕头市民约有1500人.
15. 如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )
如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )
 如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )
如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠BED的大小为( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 45° |
12.下列各式中,正确的是( )
| A. | $\root{3}{-5}$=-$\root{3}{5}$ | B. | $\sqrt{16}$=±4 | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{3.6}$=0.6 |
 在矩形纸片ABCD中,AB=4,BC=6,将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是2.5.
在矩形纸片ABCD中,AB=4,BC=6,将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是2.5.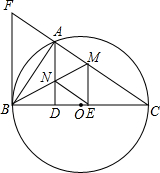 如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC.
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC.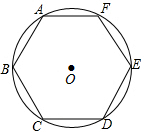 如图,已知正六边形ABCDEF没接于半径为4的⊙O,则B、D两点间的距离为4$\sqrt{3}$.
如图,已知正六边形ABCDEF没接于半径为4的⊙O,则B、D两点间的距离为4$\sqrt{3}$.