题目内容
18.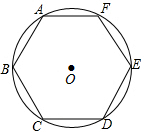 如图,已知正六边形ABCDEF没接于半径为4的⊙O,则B、D两点间的距离为4$\sqrt{3}$.
如图,已知正六边形ABCDEF没接于半径为4的⊙O,则B、D两点间的距离为4$\sqrt{3}$.
分析 连接OB,OC,OD,BD交OC于P,根据已知条件得到∠BOD=120°,$\widehat{BC}$=$\widehat{CD}$,由垂径定理得到OC⊥BD,根据等腰三角形的性质得到∠OBD=30°,于是得到结论.
解答 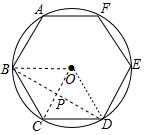 解:连接OB,OC,OD,BD交OC于P,
解:连接OB,OC,OD,BD交OC于P,
∴∠BOC=∠COD=60°,
∴∠BOD=120°,$\widehat{BC}$=$\widehat{CD}$,
∴OC⊥BD,
∵OB=OD,
∴∠OBD=30°,
∵OB=4,
∴PB=$\frac{\sqrt{3}}{2}$OB=2$\sqrt{3}$,
∴BD=2PB=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$.
点评 此题主要考查了正多边形和圆,解答此题的关键是熟知正六边形的边长等于半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.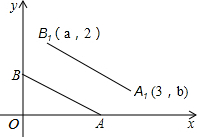 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )| A. | 1,3 | B. | 1,2 | C. | 2,1 | D. | 1,1 |
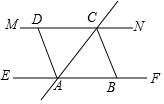 已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.
已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.