题目内容
8.若M=(x-3)(x-5),N=(x-2)(x-6),则M与N的大小关系为m>N.分析 根据题目中的M和N,可以得到M-N的值,然后与0比较大小,即可解答本题.
解答 解:∵M=(x-3)(x-5),N=(x-2)(x-6),
∴M-N
=(x-3)(x-5)-(x-2)(x-6)
=x2-8x+15-x2+8x-12
=3>0,
∴M>N,
故答案为:M>N.
点评 本题考查多项式的减法、比较数的大小,解答本题的关键是明确多项式减法的计算方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.化简$\frac{x}{x-y}$$-\frac{y}{x+y}$的结果为( )
| A. | $\frac{2xy}{{x}^{2}-{y}^{2}}$ | B. | $-\frac{2xy}{{x}^{2}-{y}^{2}}$ | C. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | D. | 1 |
18.将0.0000026用科学记数法表示为( )
| A. | 2.6×106 | B. | 0.26×10-5 | C. | 2.6×10-6 | D. | 2.6×10-7 |
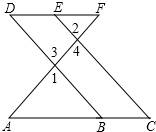 完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.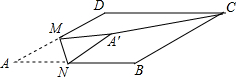 如图,在平行四边形ABCD中,∠BCD=30°,BC=6,CD=$6\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线
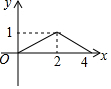
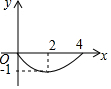
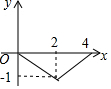
如图,在平行四边形ABCD中,∠BCD=30°,BC=6,CD=$6\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线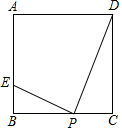 如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )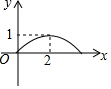
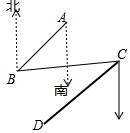 如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.