题目内容
18.已知:方程x2-kx+1=0有两个相等的实数根且反比例函数y=$\frac{k-1}{x}$ 的图象在第一、三象限,则k的值为2.分析 根据判别式的意义得到△=k2-4=0,解得k=±2,在根据反比例函数性质得到k-1>0,解得k>1,两者结合求得k的值即可.
解答 解:∵方程x2-kx+1=0有两个相等的实数根,
∴△=k2-4=0,解得k=±2,
∵反比例函数y=$\frac{k-1}{x}$ 的图象在第一、三象限,
∴k-1>0,解得k>1,
∴k的值为2.
故答案为:2.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了反比例函数性质.

练习册系列答案
相关题目
8.某食品厂从生产的袋装食品中抽出20袋检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数表示,记录如下表:
这批样品的平均质量比标准质量多还是少?多或少几克?若标准质量为450克/袋,则抽样检测总质量是多少?
| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 5 |
| 袋数 | 1 | 4 | 2 | 4 | 5 | 4 |
9.一次科技知识竞赛,两个班学生的成绩如下:
(1)请分别求出两个班成绩的众数与中位数.
(2)若规定100分为一等奖,90分为二等奖,80分为三等奖,请分别求出两个班的获奖率.
(3)请分别求出两个班成绩的方差.
| 分数(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 甲班人数(人) | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙班人数(人) | 4 | 4 | 16 | 2 | 12 | 12 |
(2)若规定100分为一等奖,90分为二等奖,80分为三等奖,请分别求出两个班的获奖率.
(3)请分别求出两个班成绩的方差.
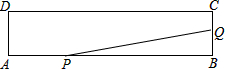 如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2).
如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2).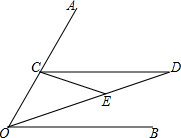 已知∠AOB,点C是OA上任意一点,CD∥OB,且∠AOE=∠CEO,∠DCE=∠D,试说明∠DOB=$\frac{1}{3}$∠AOB.
已知∠AOB,点C是OA上任意一点,CD∥OB,且∠AOE=∠CEO,∠DCE=∠D,试说明∠DOB=$\frac{1}{3}$∠AOB.