题目内容
8.先化简,再求值:($\frac{2}{a-1}$-$\frac{2a+1}{{a}^{2}-1}$)÷$\frac{1}{a-1}$,其中a=2sin60°-tan45°.分析 将原式括号内通分、将除法转化为乘法,再计算减法,最后约分即可化简原式,根据特殊锐角三角函数值求得a的值,代入即可.
解答 解:原式=[$\frac{2a+2}{(a+1)(a-1)}$-$\frac{2a+1}{(a+1)(a-1)}$]•(a-1)
=$\frac{1}{(a+1)(a-1)}$•(a-1)
=$\frac{1}{a+1}$
当a=2sin60°-tan45°=2×$\frac{\sqrt{3}}{2}$-1=$\sqrt{3}$-1时,
原式=$\frac{1}{\sqrt{3}-1+1}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键,也考查了特殊锐角的三角函数值.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
18.快递公司2014年的快递业务量为2亿件,受益于经济的快速增长及电子商务发展等多重因素,快递业务迅猛发展,2016年的快递业务量达到3.92亿件.若设该地区这两年快递业务量的年平均增长率为x,则下列方程正确的是( )
| A. | 2(1-x)2=3.92 | B. | 3.92(1-x)2=2 | C. | 2(1+x)2=3.92 | D. | 3.92(1+x)2=2 |
18. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )| A. | AB=AD | B. | BC=CD | C. | $\widehat{AB}=\widehat{AD}$ | D. | ∠BCA=∠DCA |
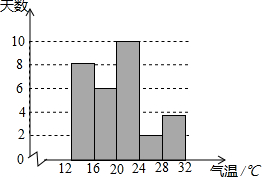 为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.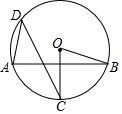 如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.
如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度. 如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( )
如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( )


