题目内容
13.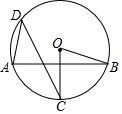 如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.
如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.
分析 首先利用垂径定理证明,$\widehat{AC}$=$\widehat{BC}$,推出∠AOC=∠COB=70°,可得∠ADC=$\frac{1}{2}$AOC=35°.
解答 解:如图,连接OA.
∵OC⊥AB,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠AOC=∠COB=70°,
∴∠ADC=$\frac{1}{2}$AOC=35°,
故答案为35.
点评 本题考查圆周角定理、垂径定理等知识,解题的关键是学会添加常用辅助线,用转化的思想思考问题.

练习册系列答案
相关题目
4. 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
(1)①在扇形图中,C部门所对应的圆心角的度数为108°
②在统计表中,b=9,c=6
(2)求这个公司平均每人所创年利润.
 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表
| 部门 | 员工人数 | 每人所创的年利润/万元 |
| A | 5 | 10 |
| B | b | 8 |
| C | c | 5 |
②在统计表中,b=9,c=6
(2)求这个公司平均每人所创年利润.
1.我市冬季里某一天的最低气温是-10℃,最高气温是5℃,这一天的温差为( )
| A. | -5℃ | B. | 5℃ | C. | 10℃ | D. | 15℃ |
5. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )| A. | ∠1=∠3 | B. | ∠2+∠4=180° | C. | ∠1=∠4 | D. | ∠3=∠4 |
2. 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
 如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )
如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |

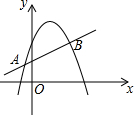 如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.