题目内容
16.在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)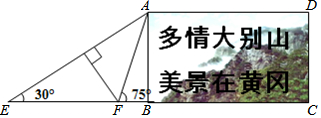
分析 如图作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,推出AH=HF,设AH=HF=x,则EF=2x,EH=$\sqrt{3}$x,在Rt△AEB中,由∠E=30°,AB=5米,推出AE=2AB=10米,可得x+$\sqrt{3}$x=10,解方程即可.
解答 解:如图 作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,
作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,
∴AH=HF,设AH=HF=x,则EF=2x,EH=$\sqrt{3}$x,
在Rt△AEB中,∵∠E=30°,AB=5米,
∴AE=2AB=10米,
∴x+$\sqrt{3}$x=10,
∴x=5$\sqrt{3}$-5,
∴EF=2x=10$\sqrt{3}$-10≈7.3米,
答:E与点F之间的距离为7.3米.
点评 本题考查解直角三角形的应用-仰角俯角问题、锐角三角函数、等腰直角三角形的性质、一元一次方程等知识,解题的关键是学会添加常用辅助线,构建方程解决问题.

练习册系列答案
相关题目
7.一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
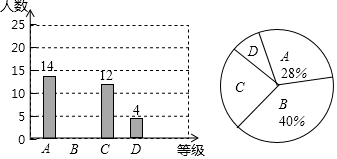
4. 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
(1)①在扇形图中,C部门所对应的圆心角的度数为108°
②在统计表中,b=9,c=6
(2)求这个公司平均每人所创年利润.
 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图各部门人数及每人所创年利润统计表
| 部门 | 员工人数 | 每人所创的年利润/万元 |
| A | 5 | 10 |
| B | b | 8 |
| C | c | 5 |
②在统计表中,b=9,c=6
(2)求这个公司平均每人所创年利润.
1.我市冬季里某一天的最低气温是-10℃,最高气温是5℃,这一天的温差为( )
| A. | -5℃ | B. | 5℃ | C. | 10℃ | D. | 15℃ |
5. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )| A. | ∠1=∠3 | B. | ∠2+∠4=180° | C. | ∠1=∠4 | D. | ∠3=∠4 |
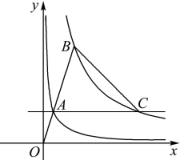 如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.
如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.