题目内容
13．
如图，正方形ABCD的边长为8，点M在边DC上，且DM=2，点N是边AC上一动点，则线段DN+MN的最小值为（ ）| A． | 8 | B． | 8$\sqrt{2}$ | C． | 2$\sqrt{17}$ | D． | 10 |
分析 要使DN+MN最小，首先应分析点N的位置．根据正方形的性质：正方形的对角线互相垂直平分．知点D的对称点是点B，连接MB交AC于点N，此时DN+MN最小值即是BM的长．
解答 解：根据题意，连接BD、BM，则BM就是所求DN+MN的最小值，
在Rt△BCM中，BC=8，CM=6
根据勾股定理得：BM=$\sqrt{{6}^{2}+{8}^{2}}$=10，
即DN+MN的最小值是10；
故选D．
点评 此题考查轴对称问题，此题的难点在于确定满足条件的点N的位置：利用轴对称的方法．然后熟练运用勾股定理．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如图，在△ABC中，已知AB=AC，∠A=45°，BD⊥AC于点D．根据该图可以求出tan22.5°=$\sqrt{2}$-1．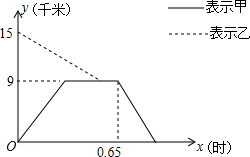
乙骑摩托车与B城相距15千米的A城办事，为了节省时间，甲同时从A城开车出发，先到达C城的D处，并在C城用了12分钟加油回到D处，此时乙已经到达D处等候甲3分钟了，乙把摩托车放到D处，乘甲开的汽车去A城，他们与A城的距离y千米与时间x之间的关系如图，回答下列问题：
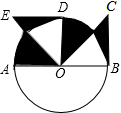如图，AB是⊙O的直径，过点B作BC⊥OB，且BC=OB，点C在AB的上方，连接OC，△OBC绕着点O逆时针旋转90°得到△ODE
3．下列各实数中，最小的是（ ）
| A． | -π | B． | （-1）0 | C． | $\root{3}{-1}$ | D． | |-2| |