题目内容
4．若实数a满足a2+a=1，则-2a2-2a+2015=2013．分析 首先化简所给代数式-2a2-2a+2015，然后把a2+a=1代入算式-2a2-2a+2015，求出算式的值是多少即可．
解答 解：∵a2+a=1，
∴-2a2-2a+2015
=-2（a2+a）+2015
=-2×1+2015
=-2+2015
=2013
故答案为：2013．
点评 此题主要考查了代数式的求值问题，采用代入法即可，要熟练掌握，题型简单总结以下三种：①已知条件不化简，所给代数式化简；②已知条件化简，所给代数式不化简；③已知条件和所给代数式都要化简．
练习册系列答案
相关题目
19．在平面直角坐标系中，点P（-2，3）关于y轴的对称点的坐标（ ）
| A． | （-2，-3） | B． | （2，-3） | C． | （-2，3） | D． | （2，3） |
16．已知a+$\frac{1}{a}$=4，则a2+$\frac{1}{a^2}$的值是（ ）
| A． | 4 | B． | 16 | C． | 14 | D． | 15 |
13．
如图，正方形ABCD的边长为8，点M在边DC上，且DM=2，点N是边AC上一动点，则线段DN+MN的最小值为（ ）
如图，正方形ABCD的边长为8，点M在边DC上，且DM=2，点N是边AC上一动点，则线段DN+MN的最小值为（ ）| A． | 8 | B． | 8$\sqrt{2}$ | C． | 2$\sqrt{17}$ | D． | 10 |
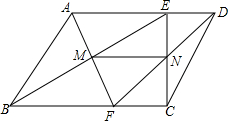如图，在平行四边形ABCD中，E，F分别是AD，BC上的点，且AE=BF，BE交AF于M，CE交DF于N，求证：MN$\stackrel{∥}{=}$$\frac{1}{2}$AD．