题目内容
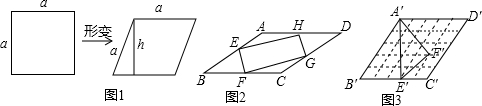
7.如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把a与h的比值叫做这个菱形的“形变度”.(1)当形变后的菱形有一个内角是60°时,则这个菱形的“形变度”为$\frac{2\sqrt{3}}{3}$.
(2)如图2,菱形ABCD的“形变度”为$\sqrt{5}$.
①这个菱形形变前与形变后的面积之比为$\sqrt{5}$.
②点E、F、G、H分别是菱形ABCD各边的中点,求四边形EFGH形变前与形变后的面积之比.
(3)一个正方形ABCD由边长为1的5×5网格小正方形组成,形变后成为菱形A′B′C′D′如图3,原正方形内的△AEF(E、F是小正方形的顶点),同时形变为△A′E′F′,已知这个菱形的“形变度”为$\frac{5}{4}$,则形变后的△A′E′F′的面积为4.4.
分析 (1)在直角三角形中,由∠B=60°,在Rt△ABC中,利用正弦函数求得;
(2)①求出形变前正方形的面积,形变后菱形的面积,两面积之比即为所求;
②分别表示出四边形EFGH形变前与形变后的面积,进而得出答案;
(3)利用(2)中所求得出两个四边形的面积比,即可得出答案.
解答 解:(1)由题意得,∠B=60°,
在Rt△ABC中,∠B=60°,
∴h=AC=ABsin∠B=$\frac{\sqrt{3}}{2}$a,
∴k=$\frac{a}{h}$=$\frac{2\sqrt{3}}{3}$;
故答案为:$\frac{{2\sqrt{3}}}{3}$;
(2)①形变前的面积=a2,
∵k=$\sqrt{5}$,∴$\frac{a}{h}$=$\sqrt{5}$,
∴h=$\frac{\sqrt{5}a}{5}$,
∴形变后的面积=a•$\frac{\sqrt{5}a}{5}$=$\frac{\sqrt{5}}{5}$a2
∴菱形形变前的面积与形变后的面积之比:$\frac{{a}^{2}}{\frac{\sqrt{5}{a}^{2}}{5}}$=$\sqrt{5}$;
故答案为:$\sqrt{5}$;
②∵点E,F,G,H是四边形ABCD各边的中点,
∴四边形EFGH形变前的面积为$\frac{1}{2}$a2,
∵EH是△ABD的中位线,
∴EH=$\frac{1}{2}$BD,同理EF=$\frac{1}{2}$AC,
∵四边形EFGH是矩形,
∴矩形EFGH的面积=$\frac{1}{2}$BD×$\frac{1}{2}$AC=$\frac{1}{2}$S四边形ABCD=$\frac{1}{2}$ah,
∴四边形EFGH形变前的面积与形变后的面积之比是:$\frac{\frac{1}{2}{a}^{2}}{\frac{1}{2}ah}$=$\frac{a}{h}$=$\sqrt{5}$,
(3)如图3所示:∵这个菱形的“形变度”为$\frac{5}{4}$,
∴菱形形变前的面积与形变后的面积之比:$\frac{5}{4}$,
∵S△AEF=25-$\frac{1}{2}$×3×5-5-$\frac{1}{2}$×1×2-$\frac{1}{2}$×3×4=5.5,
∴S△A′E′F′=4.4.
故答案为:4.4.
点评 本题考查了正方形的性质,菱形的性质以及四边形综合,根据题意得出菱形形变前的面积与形变后的面积之比是解题关键.

 小明一家驾车从家出发到某景区游玩,玩了一段时间后,又驾车回家,图中的折线OABC反映了小明一家离家的距离y(千米)与离家时间x(小时)之间的函数关系图象,请根据图中信息解答下列问题:
小明一家驾车从家出发到某景区游玩,玩了一段时间后,又驾车回家,图中的折线OABC反映了小明一家离家的距离y(千米)与离家时间x(小时)之间的函数关系图象,请根据图中信息解答下列问题: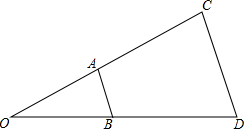 如图,△OAB和△COD是位似图形,AB与CD平行么?
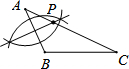
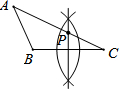
如图,△OAB和△COD是位似图形,AB与CD平行么? 如图,已知△ABC(AB<BC<AC),用尺规在AC上确定一点P,使PB+PC=AC,则下列选项中,一定符合要求的作图痕迹是( )
如图,已知△ABC(AB<BC<AC),用尺规在AC上确定一点P,使PB+PC=AC,则下列选项中,一定符合要求的作图痕迹是( )