题目内容
3.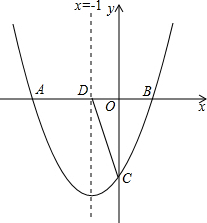 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)(1)求抛物线的解析式.
(2)设抛物线与y轴的交点为C,对称轴与x轴交于D,抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?若存在,求出P点坐标;若不存在,说明理由.
分析 (1)根据对称轴与A点坐标可立即求出B点坐标,再根据A、B两点坐标求出解析式;
(2)分类讨论:①以C为等腰三角形的顶点;②以D为等腰三角形的顶点.
解答 解:(1)∵抛物线的对称轴为x=-1,A(-3,0)为抛物线与x轴的交点,B为另一个交点,
∵B(1,0),
将A、B两点坐标代入抛物线解析式得:$\left\{\begin{array}{l}{1+b+c=0}\\{9-3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=-3}\end{array}\right.$,
∴抛物线的解析式为y=x2+2x-3;
(2)∵D(-1,0),C(0,-3),
∴CD=$\sqrt{10}$,
①若DC=DP,如图1,
此时P点的坐标为:(-1,$\sqrt{10}$)、(-1,$-\sqrt{10}$);
②若CD=CP,如图2,
此时P点的坐标为:(-1,-6);
综上所述,满足要求的P点坐标有:(-1,$\sqrt{10}$)、(-1,$-\sqrt{10}$)、(-1,-6).
点评 本题考查了待定系数法二次函数解析式、勾股定理、等腰三角形的性质等知识点,是一道基础题.第(2)问体现分类讨论的思想,要注意考虑周全.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.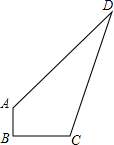 某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,AD=13m,CD=12m,若每种植1平方米草皮需要150元,问总共需要投入多少元?
某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,AD=13m,CD=12m,若每种植1平方米草皮需要150元,问总共需要投入多少元?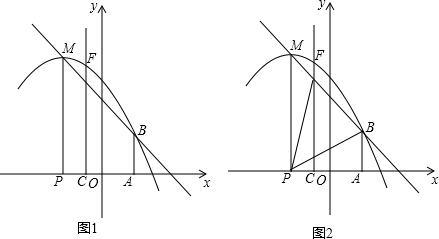
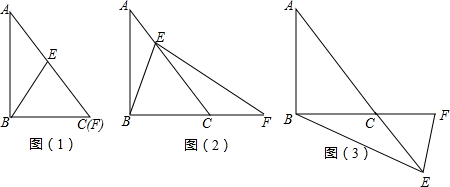
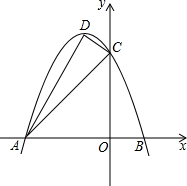 已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.
已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.