题目内容
已知△ABC为等边三角形,D为AB的中点,E在AC上,CE<BD,作∠EDF=60°,交BC于点F,求证:BD-CE=EF-BF.
考点:全等三角形的判定与性质,等边三角形的性质,三角形中位线定理
专题:
分析:作DM∥BC交AC于M,延长CB至N,使BN=EM,证出△DBN≌△DME,推出DN=DE,∠BDN=∠MDE,求出∠FDN=∠EDF,证出△FDN≌△FDE,推出EF=NF,即可得出答案.
解答: 证明:作DM∥BC交AC于M,延长CB至N,使BN=EM,
证明:作DM∥BC交AC于M,延长CB至N,使BN=EM,
∵等边三角形ABC中,D为AB中点,DM∥BC,
∴DM是△ABC的中位线,BD=
AB=
BC,∠BDM=∠DME=120°,∠ABC=60°,
∴DM=
BC=BD=CM,∠DBN=∠DME=120°,
在△DBN和△DME中
∴△DBN≌△DME(SAS),
∴DN=DE,∠BDN=∠MDE,
∴∠EDF=60°,∠BDM=120°,
∴∠FDN=∠FDB+∠NDB=∠FDB+∠MDE=60°=∠EDF,
在△FDN和△FDE中,
,
∴△FDN≌△FDE(SAS),
∴EF=NF,
即EF-BF=NF-BF=BN,BD-CE=CM-CME=BN,
∴BD-CE=EF-BF.
 证明:作DM∥BC交AC于M,延长CB至N,使BN=EM,
证明:作DM∥BC交AC于M,延长CB至N,使BN=EM,∵等边三角形ABC中,D为AB中点,DM∥BC,
∴DM是△ABC的中位线,BD=
| 1 |
| 2 |
| 1 |
| 2 |
∴DM=
| 1 |
| 2 |
在△DBN和△DME中
|
∴△DBN≌△DME(SAS),
∴DN=DE,∠BDN=∠MDE,
∴∠EDF=60°,∠BDM=120°,
∴∠FDN=∠FDB+∠NDB=∠FDB+∠MDE=60°=∠EDF,
在△FDN和△FDE中,
|
∴△FDN≌△FDE(SAS),
∴EF=NF,
即EF-BF=NF-BF=BN,BD-CE=CM-CME=BN,
∴BD-CE=EF-BF.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,三角形的中位线的应用,题目比较好,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,下图形绕直线l旋转360°后,能得到圆柱体的是( )
A、 |
B、 |
C、 |
D、 |
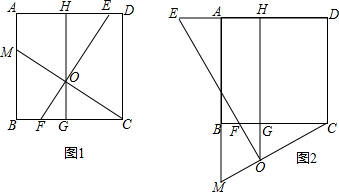
 如图,在平行四边形ABCD中,E是BC中点,AF⊥CD于点F,AE=4,AF=6,则△AEF的面积是
如图,在平行四边形ABCD中,E是BC中点,AF⊥CD于点F,AE=4,AF=6,则△AEF的面积是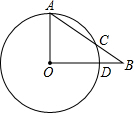 如图,在Rt△AOB中,∠AOB=90°,以OA为半径的圆交AB于点C.若AO=5,OB=12,求BC的长.
如图,在Rt△AOB中,∠AOB=90°,以OA为半径的圆交AB于点C.若AO=5,OB=12,求BC的长. 在数轴上画出表示
在数轴上画出表示