题目内容
9.将抛物线y=x2-2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )| A. | y=(x-1)2+4 | B. | y=(x-4)2+4 | C. | y=(x+2)2+6 | D. | y=(x-4)2+6 |
分析 根据函数图象向上平移加,向右平移减,可得函数解析式.
解答 解:将y=x2-2x+3化为顶点式,得y=(x-1)2+2.
将抛物线y=x2-2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为y=(x-4)2+4,
故选:B.
点评 本题考查了二次函数图象与几何变换,函数图象的平移规律是:左加右减,上加下减.

练习册系列答案
相关题目
17.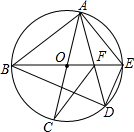 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )| A. | △ABE | B. | △ACF | C. | △ABD | D. | △ADE |
14. 将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( )
将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( )
 将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( )
将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( )| A. | $\frac{8}{3}\sqrt{3}$cm2 | B. | 8cm2 | C. | $\frac{16}{3}\sqrt{3}$cm2 | D. | 16cm2 |
18.计算:cos245°+sin245°=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
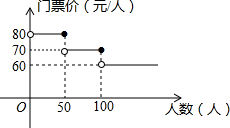 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元. 在平面直角坐标系中,已知点A(-3,1),B(-2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.
在平面直角坐标系中,已知点A(-3,1),B(-2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.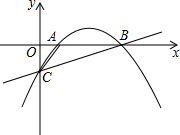 如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.
如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.