题目内容
19.设⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.分析 根据直线和圆的位置关系得出d=r,根据根与系数的关系得出△=0,代入求出即可.
解答 解:∵⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切,
∴d=r,
∵d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,
∴△=0,
即[-(m+6)]2-4(m+9)•1=0,
解得:m=0或-8,
当m=-8时,x=-1,不符合题意舍去,
故m=0.
点评 本题考查了直线和圆的位置关系和根与系数的关系的应用,解此题的关键是得出关于m的一元二次方程,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (a+b)(a-b)=a2-b2 | C. | (a3)2=a5 | D. | a3÷a3=a |
9.将抛物线y=x2-2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )
| A. | y=(x-1)2+4 | B. | y=(x-4)2+4 | C. | y=(x+2)2+6 | D. | y=(x-4)2+6 |
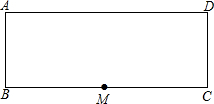 如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.
如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.
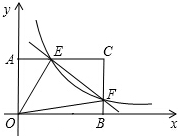 在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)图象与AC边交于点E.
在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)图象与AC边交于点E.