题目内容
1.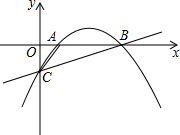 如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.
如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
分析 (1)把A、B两点分别代入抛物线解析可求得a和b,可求得抛物线解析式;
(2)过A作AD⊥BC于点D,则AD为⊙A的半径,由条件可证明△ABD∽△CBO,利用相似三角形的性质可求得AD的长,可求得半径;
(3)由待定系数法可求得直线BC解析式,过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,可设出P、Q的坐标,可表示出△PQC和△PQB的面积,可表示出△PBC的面积,再利用二次函数的性质可求得其最大值,容易求得P点坐标.
解答 解:(1)∵抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得$\left\{\begin{array}{l}{a+b-\frac{5}{3}=0}\\{25a+5b-\frac{5}{3}=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{3}$x2+2x-$\frac{5}{3}$;
(2)过A作AD⊥BC于点D,如图1,
∵⊙A与BC相切,
∴AD为⊙A的半径,
由(1)可知C(0,-$\frac{5}{3}$),且A(1,0),B(5,0),
∴OB=5,AB=OB-OA=4,OC=$\frac{5}{3}$,
在Rt△OBC中,由勾股定理可得BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{(\frac{5}{3})^{2}+{5}^{2}}$=$\frac{5\sqrt{10}}{3}$,
∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,
∴$\frac{AD}{OC}$=$\frac{AB}{BC}$,即$\frac{AD}{\frac{5}{3}}$=$\frac{4}{\frac{5\sqrt{10}}{3}}$,解得AD=$\frac{2\sqrt{10}}{5}$,
即⊙A的半径为$\frac{2\sqrt{10}}{5}$;
(3)∵C(0,-$\frac{5}{3}$),
∴可设直线BC解析式为y=kx-$\frac{5}{3}$,
把B点坐标代入可求得k=$\frac{1}{3}$,
∴直线BC的解析式为y=$\frac{1}{3}$x-$\frac{5}{3}$,
过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,如图2,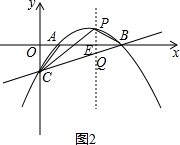
设P(x,-$\frac{1}{3}$x2+2x-$\frac{5}{3}$),则Q(x,$\frac{1}{3}$x-$\frac{5}{3}$),
∴PQ=(-$\frac{1}{3}$x2+2x-$\frac{5}{3}$)-($\frac{1}{3}$x-$\frac{5}{3}$)=-$\frac{1}{3}$x2+$\frac{5}{3}$x=-$\frac{1}{3}$(x-$\frac{5}{2}$)2+$\frac{25}{12}$,
∴S△PBC=S△PCQ+S△PBQ=$\frac{1}{2}$PQ•OE+$\frac{1}{2}$PQ•BE=$\frac{1}{2}$PQ(OE+BE)=$\frac{1}{2}$PQ•OB=$\frac{5}{2}$PQ=-$\frac{5}{6}$(x-$\frac{5}{2}$)2+$\frac{125}{24}$,
∴当x=$\frac{5}{2}$时,S△PBC有最大值$\frac{125}{24}$,此时P点坐标为($\frac{5}{2}$,$\frac{5}{4}$),
∴当P点坐标为($\frac{5}{2}$,$\frac{5}{4}$)时,△PBC的面积有最大值.
点评 本题主要考查二次函数的综合应用,涉及待定系数法、切线的性质、相似三角形的判定和性质、二次函数的性质等知识.在(1)中注意待定系数法的应用步骤,在(2)中确定出⊙A的半径是解题的关键,在(3)中用P点坐标表示出△PBC的面积是解题的关键.本题考查知识点较多,计算量大,综合性较强.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y=(x-1)2+4 | B. | y=(x-4)2+4 | C. | y=(x+2)2+6 | D. | y=(x-4)2+6 |
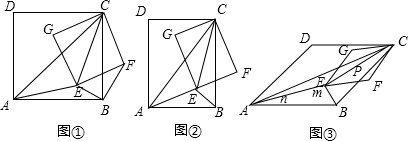
 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )
如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )| A. | 1:2 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
 某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )
某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )| A. | 21,21 | B. | 21,21.5 | C. | 21,22 | D. | 22,22 |
| A. | 57000000=57×106 | |
| B. | 0.0158(用四舍五入法精确到0.001)=0.015 | |
| C. | 1.804(用四舍五入法精确到十分位)=1.8 | |
| D. | 0.0000257=2.57×10-4 |
 如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.
如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2. 如图是一个正方体纸盒的展开图,其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”,将其围成一个正方体后,则与“5”相对的是( )
如图是一个正方体纸盒的展开图,其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”,将其围成一个正方体后,则与“5”相对的是( )