题目内容
1.八(2)班组织了一次经典朗读比赛,甲、乙两队各5人的比赛成绩如下表(10分制):| 甲 | 10 | 8 | 9 | 8 | 10 |
| 乙 | 9 | 10 | 7 | 10 | 9 |
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是0.8分2,则成绩较为整齐的是甲队.
分析 (1)利用中位数和众数的定义求解;
(2)根据平均数和方差的定义计算;
(3)根据方差的意义进行判断.
解答 解:(1)甲队成绩的中位数是9分,乙队成绩的众数是10分;
(2)乙队的平均成绩=$\frac{1}{5}$(9+10+7+10+9)=9,
乙队的方差=$\frac{1}{5}$[(9-9)2+(10-9)2+(7-9)2+(10-9)2+(9-9)2]=1.2;
(3)因为0.8<1.2,
所以甲成绩较为整齐.
点评 本题考查了方差:方差的计算公式是:s2=$\frac{1}{n}$[(x1-x?)2+(x2-x?)2+…+(xn-x?)2](可简单记忆为“方差等于差方的平均数”);方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数、中位数和众数.

练习册系列答案
相关题目
12.下列四个等式从左到右的变形,是多项式的因式分解的是( )
| A. | (x+3)(x-3)=x2-9 | B. | a2b+ab2=ab(a+b) | ||
| C. | x2-3x+1=x(x-3)+1 | D. | ${m^2}-2m-1=m(m-2-\frac{1}{m})$ |
9.北盘江旅游景点在2017年6月4日至6月14日蓄水期间,水位由106米直升至135米,是划船旅游最佳的时期,设水位匀速上生,那么下列图象中,能反应这10天水位h(米)随时间t(天)变化的是( )
| A. |  | B. | 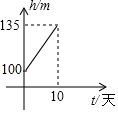 | C. | 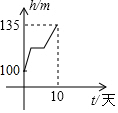 | D. | 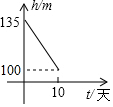 |
13.商场进了一批商品,进价为每件800元,如果要保持销售利润不低于15%,则售价应不低于( )
| A. | 900元 | B. | 920元 | C. | 960元 | D. | 980元 |
11. 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )
 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )| A. | 6 | B. | 4 | C. | 64 | D. | 8 |
 如图,在平行四边形ABCE中,点D是AE上的一点,且CE=CD,求证:∠DCB=∠B.
如图,在平行四边形ABCE中,点D是AE上的一点,且CE=CD,求证:∠DCB=∠B.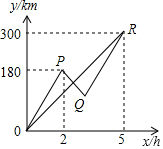 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.