题目内容
9.在△ABC中,∠C=90°,∠B=30°,O为AB上一点,OA=m,⊙O的半径r=$\frac{1}{2}$.在下列条件下,分别求m的取值范围.(1)AC与⊙O相离.
(2)AC与⊙O相切.
(3)AC与⊙0相交.
分析 根据点到的距离d,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离解答.
解答  解:作OD⊥AC于D,
解:作OD⊥AC于D,
当OD=$\frac{1}{2}$时,
∵∠C=90°,OD⊥BC,
∴OD∥BC,
∴∠DOA=∠B=30°,
∴cos30°=$\frac{\frac{1}{2}}{m}$,
解得m=$\frac{\sqrt{3}}{3}$,
(1)当m>$\frac{\sqrt{3}}{3}$时,AC与⊙O相离;
(1)当m=$\frac{\sqrt{3}}{3}$时,AC与⊙O相切;
(1)当m<$\frac{\sqrt{3}}{3}$时,AC与⊙O相交.
点评 本题考查的是直线与圆的位置关系,掌握点到的距离d,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
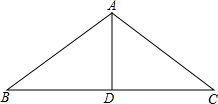 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.