题目内容
9.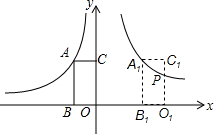 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
分析 先求出A点坐标,再根据图形平移的性质得出A1点的坐标,故可得出反比例函数的解析式,把O1点的横坐标代入即可得出结论.
解答 解:∵OB=1,AB⊥OB,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,
∴当x=-1时,y=2,
∴A(-1,2).
∵此矩形向右平移3个单位长度到A1B1O1C1的位置,
∴B1(2,0),
∴A1(2,2).
∵点A1在函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=4,
∴反比例函数的解析式为y=$\frac{4}{x}$,O1(3,0),
∵C1O1⊥x轴,
∴当x=3时,y=$\frac{4}{3}$,
∴P(3,$\frac{4}{3}$).
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.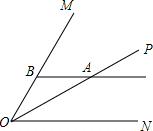 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )
 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 6 |
18. 如图,∠A=60°,∠B=80°,则∠1+∠2=( )
如图,∠A=60°,∠B=80°,则∠1+∠2=( )
 如图,∠A=60°,∠B=80°,则∠1+∠2=( )
如图,∠A=60°,∠B=80°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 140° | D. | 150° |
19.下列各式不正确的是( )
| A. | 18000″<360′ | B. | 2°30′>2.4° | C. | 36000″<8° | D. | 1°10′20″>4219″ |
 如图,矩形ABCD中,BC=2,DC=4,以AB为直径的半圆O与DC相切于点E,则阴影部分的面积为多少?(结果保留π)
如图,矩形ABCD中,BC=2,DC=4,以AB为直径的半圆O与DC相切于点E,则阴影部分的面积为多少?(结果保留π) 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有4个.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有4个.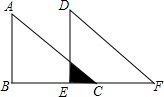 如图,等腰直角三角形ABC中,∠ABC=90°,AB=BC=4cm,将△ABC沿BC方向平移3cm后,得△DEF,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,等腰直角三角形ABC中,∠ABC=90°,AB=BC=4cm,将△ABC沿BC方向平移3cm后,得△DEF,则图中阴影部分的面积为$\frac{1}{2}$cm2.