题目内容
17．
如图，矩形ABCD中，BC=2，DC=4，以AB为直径的半圆O与DC相切于点E，则阴影部分的面积为多少？（结果保留π）
分析 连接OE．先求空白部分BCE的面积，再用△BCD的面积-空白部分BCE的面积得阴影面积．
解答 
解：连接OE．
阴影部分的面积=S△BCD-（S正方形OBCE-S扇形OBE）=$\frac{1}{2}$×2×4-（2×2-$\frac{1}{4}$π×2×2）=π．
答：阴影部分的面积为π．
点评 本题考查了三角形的面积、矩形的性质、切线的性质的应用，关键是能把求不规则图形的面积转化成求规则图形的面积，题目比较典型，主要培养了学生的计算能力．
练习册系列答案
相关题目
12．
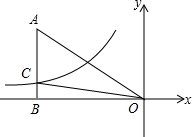如图，已知双曲线y=$\frac{k}{x}$（k＜0）经过Rt△AOB斜边AO的中点D，且与直角边AB相交于点C．若点A的坐标为（-6，4），则△AOC的面积为（ ）
如图，已知双曲线y=$\frac{k}{x}$（k＜0）经过Rt△AOB斜边AO的中点D，且与直角边AB相交于点C．若点A的坐标为（-6，4），则△AOC的面积为（ ）| A． | 8 | B． | 9 | C． | 10 | D． | 18 |
2．三角形两边长分别为3和6，第三边的长是方程x2-15x+50=0的两根，则该三角形的周长为（ ）
| A． | 14 | B． | 15 | C． | 19 | D． | 14或19 |
9．
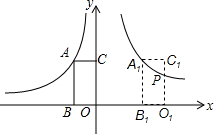如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=-$\frac{2}{x}$（x＜0）的图象上，将此矩形向右平移3个单位长度到A1B1O1C1的位置，此时点A1在函数y=$\frac{k}{x}$（x＞0）的图象上，C1O1与此图象交于点P，则点P的纵坐标是（ ）
如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=-$\frac{2}{x}$（x＜0）的图象上，将此矩形向右平移3个单位长度到A1B1O1C1的位置，此时点A1在函数y=$\frac{k}{x}$（x＞0）的图象上，C1O1与此图象交于点P，则点P的纵坐标是（ ）| A． | $\frac{5}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $\frac{2}{3}$ |