题目内容
18．
如图，∠A=60°，∠B=80°，则∠1+∠2=（ ）| A． | 100° | B． | 120° | C． | 140° | D． | 150° |
分析 在四边形ABCD中，根据四边形的内角和定理和邻补角的定义就可以得到∠1+∠2的度数．
解答 解：∵∠A=60°，∠B=80°，
∴∠ADC+∠BCD=220°，
∴∠1+∠2=360°-220°=140°．
故选C．
点评 本题主要考查了四边形的内角和定理，以及邻补角的定义．四边形的内角和等于360°．
练习册系列答案
相关题目
9．
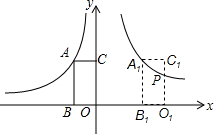如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=-$\frac{2}{x}$（x＜0）的图象上，将此矩形向右平移3个单位长度到A1B1O1C1的位置，此时点A1在函数y=$\frac{k}{x}$（x＞0）的图象上，C1O1与此图象交于点P，则点P的纵坐标是（ ）
如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=-$\frac{2}{x}$（x＜0）的图象上，将此矩形向右平移3个单位长度到A1B1O1C1的位置，此时点A1在函数y=$\frac{k}{x}$（x＞0）的图象上，C1O1与此图象交于点P，则点P的纵坐标是（ ）| A． | $\frac{5}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $\frac{2}{3}$ |
10．若|2a|=-2a，则a一定是（ ）
| A． | 正数 | B． | 负数 | C． | 非正数 | D． | 非负数 |