题目内容
20.(1)计算:-22$÷(-|-2|-\frac{1}{4})×(-1\frac{1}{2})^{2}-\frac{{4}^{2}}{3}$(2)解方程:$\frac{1}{3}$-2×($\frac{1}{6}x-2$)=$\frac{1}{2}-3×(2-\frac{1}{6}x)$.
分析 (1)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的;
(2)去分母、去括号、移项、合并同类项、系数化为1,依此即可求解.
解答 解:(1)-22$÷(-|-2|-\frac{1}{4})×(-1\frac{1}{2})^{2}-\frac{{4}^{2}}{3}$
=-4÷(-2-$\frac{1}{4}$)×$\frac{9}{4}$-$\frac{16}{3}$
=-4÷(-$\frac{9}{4}$)×$\frac{9}{4}$-$\frac{16}{3}$
=4-$\frac{16}{3}$
=-$\frac{4}{3}$;
(2)$\frac{1}{3}$-2×($\frac{1}{6}x-2$)=$\frac{1}{2}-3×(2-\frac{1}{6}x)$,
2-12×($\frac{1}{6}x-2$)=3-18(2-$\frac{1}{6}$x),
2-2x+24=3-36+3x,
-5x=-59,
x=$\frac{59}{5}$.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.
同时考查了解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
 如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )| A. | 180°-α | B. | 90°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |
12.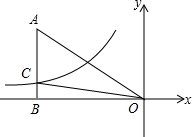 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△AOB斜边AO的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△AOB斜边AO的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )
 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△AOB斜边AO的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△AOB斜边AO的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )| A. | 8 | B. | 9 | C. | 10 | D. | 18 |
9.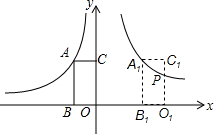 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
10.若|2a|=-2a,则a一定是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |