题目内容
19.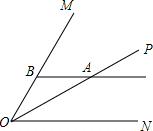 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=6,则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 6 |
分析 过点A作AE⊥OM于E,作AF⊥ON于F,根据角平分线上的点到角的两边距离相等可得AE=AF,根据两直线平行,同位角相等求出∠ABE,再求出AE,从而得解.
解答 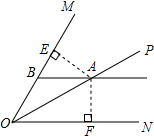 解:如图,过点A作AE⊥OM于E,作AF⊥ON于F,
解:如图,过点A作AE⊥OM于E,作AF⊥ON于F,
∵OP是∠MON的角平分线,
∴AE=AF,
∵AB∥ON,
∴∠ABE=∠MON=60°,
∴AE=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$,
∴AF=3$\sqrt{3}$,
即直线AB与ON之间的距离是3$\sqrt{3}$.
故选C.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形的性质,熟记性质是解题的关键,难点在于作出辅助线.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
4.下列等式一定成立的是( )
| A. | a2+a3=2a5 | B. | a2•a3=a5 | C. | (2ab2)3=6a3b6 | D. | a6÷a3=a2 |
9.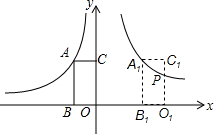 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
 如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |

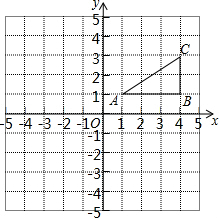 如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).