题目内容
1.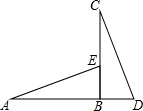 如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.判断AE与CD的数量关系和位置关系,并说明理由.
如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.判断AE与CD的数量关系和位置关系,并说明理由.
分析 延长AE交CD于F点,根据边角边判定三角形全等可以证明△ABE≌△CBD,可以证明AE=CD,∠A=∠C,进而可以证明AE⊥CD,即可解题.
解答 解:AE=CD,AE⊥CD,理由如下:
延长AE交CD于F点,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBD=90°}\\{BE=BD}\end{array}\right.$,
∴△ABE≌△CBD(SAS);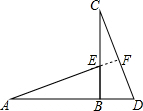
∵△ABE≌△CBD,
∴AE=CD,∠A=∠C,
∵∠C+∠CDB=90°,
∴∠A+∠CDB=90°,
∴AE⊥CD,
∴AE、CD的关系为:AE=CD,AE⊥CD
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△CBD是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列二次根式中与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{27}$ | C. | $\sqrt{30}$ | D. | $\sqrt{0.3}$ |
11.若a+b+c=0且a>b>c,则下列几个数中:a+b、ab、ab2、b2-ac、-(b+c),一定是正数的数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
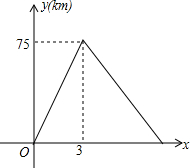 在松花江沿岸依次有A、B、C旅游景点,一观光游船由A景点顺流出发经过B景点到达C景点后立即返回,A、B两个景点之间的距离为25km,当游船到达B景点时恰好由一艘橡皮艇从B景点漂流而下,游船离开A景点的距离y(km)与其行驶时间x(h)之间的函数关系如图所示.
在松花江沿岸依次有A、B、C旅游景点,一观光游船由A景点顺流出发经过B景点到达C景点后立即返回,A、B两个景点之间的距离为25km,当游船到达B景点时恰好由一艘橡皮艇从B景点漂流而下,游船离开A景点的距离y(km)与其行驶时间x(h)之间的函数关系如图所示.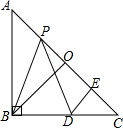 如图,Rt△ABC中,AB=BC,∠ABC=90°,O是AC边上的中点,P为AC边上一动点,D为BC上的一点,且PB=PD,DE⊥AC于E.
如图,Rt△ABC中,AB=BC,∠ABC=90°,O是AC边上的中点,P为AC边上一动点,D为BC上的一点,且PB=PD,DE⊥AC于E.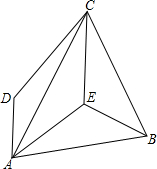 如图,在四边形ABCD中,AC平分∠DAE,DA∥CE,AB=CB.
如图,在四边形ABCD中,AC平分∠DAE,DA∥CE,AB=CB.