题目内容
9.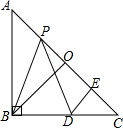 如图,Rt△ABC中,AB=BC,∠ABC=90°,O是AC边上的中点,P为AC边上一动点,D为BC上的一点,且PB=PD,DE⊥AC于E.
如图,Rt△ABC中,AB=BC,∠ABC=90°,O是AC边上的中点,P为AC边上一动点,D为BC上的一点,且PB=PD,DE⊥AC于E.(1)求证:BO=PE;
(2)设AC=10,CE=x,△ABP的面积为y,求y与x的关系.
分析 (1)根据等腰三角形的性质得到∠2=∠PBD,由等腰直角三角形的性质得到∠C=45°,推出∠1=∠C=45°,由∠3=∠PBC-∠1,∠4=∠2-∠C,得到∠3=∠4,推出△BPO≌△PDE(AAS),根据全等三角形的性质即可得到结论;
(2)根据等腰直角三角形的性质得到BO=$\frac{1}{2}$AC,于是求得BO=PE=$\frac{1}{2}$AC=5,推出AP=10-5-x,根据三角形的面积公式即可得到结论.
解答 (1)证明:∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,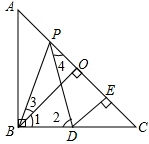
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBC-∠1,∠4=∠2-∠C,
∴∠3=∠4,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中
$\left\{\begin{array}{l}{∠3=∠4}\\{∠BOP=∠PED}\\{BP=PD}\end{array}\right.$,
∴△BPO≌△PDE(AAS),
∴BO=PE;
(2)∵AB=BC,∠ABC=90°,O是AC边上的中点,
∴BO=$\frac{1}{2}$AC,
∵BO=PE,AC=10,
∴BO=PE=$\frac{1}{2}$AC=5,∵CE=x,
∴AP=10-5-x,
∴y=$\frac{1}{2}$AP•BO=$\frac{1}{2}$(5-x)×5,
∴y与x的关系为:y=-$\frac{5}{2}$x+$\frac{25}{2}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,等腰三角形的性质,得出∠3=∠4是解题关键.

练习册系列答案
相关题目
18.下列关系中,正确的是( )
| A. | (x+3)(x+2)=x2-6 | B. | (2a-b)2=4a2-2ab+b2 | ||
| C. | (a-b)2=a2-a5-b2 | D. | (-a-b)(a-b)=b2-a2 |
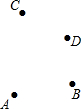 如图,已知平面内有A、B、C、D四点,按下列语句画图.
如图,已知平面内有A、B、C、D四点,按下列语句画图. 如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是D点.
如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是D点.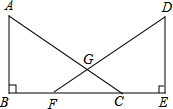 如图所示,点B、F、C、E在同一直线上,AB⊥BE、DE⊥BE.连接AC、DF,且AC=DF,AB=DE,求证:BF=CE.
如图所示,点B、F、C、E在同一直线上,AB⊥BE、DE⊥BE.连接AC、DF,且AC=DF,AB=DE,求证:BF=CE. 已知:如图,BE∥DF,AE=CF,∠A=∠C,求证:AB=CD.
已知:如图,BE∥DF,AE=CF,∠A=∠C,求证:AB=CD.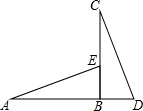 如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.判断AE与CD的数量关系和位置关系,并说明理由.
如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.判断AE与CD的数量关系和位置关系,并说明理由.