题目内容
12.从-4、$-\frac{7}{2}$、0、$\frac{7}{2}$、4这五个数中,任取一个数作为a的值,恰好使得关于x的一元二次方程2ax2-6x-1=0有两个不相等的实数根,且使两个根都在-1和1之间(包括-1和1),则取到满足条件的a值的概率为$\frac{4}{5}$.分析 分别把这5个数代入关于x的一元二次方程2ax2-6x-1=0,求出x的值,再根据概率公式即可得出结论.
解答 解:∵当a=-4时,原方程可化为-8x2-6x-1=0,解得x1=-$\frac{1}{2}$,x2=-$\frac{1}{4}$,符合题意;
当a=-$\frac{7}{2}$时,原方程可化为-7x2-6x-1=0,解得x1=-$\frac{3+\sqrt{2}}{7}$,x2=-$\frac{3-\sqrt{2}}{7}$,符合题意;
当a=0时,原方程可化为-6x-1=0,解得x1=-$\frac{1}{6}$,不符合题意;
当a=$\frac{7}{2}$时,原方程可化为7x2-6x-1=0,解得x1=1,x2=-$\frac{1}{7}$,符合题意;
当a=4时,原方程可化为8x2-6x-1=0,解得x1=-$\frac{-3+\sqrt{17}}{8}$,x2=$\frac{-3-\sqrt{17}}{8}$,符合题意.
∴取到满足条件的a值的概率=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查的是概率公式,熟知概率=所求情况数与总情况数之比是解答此题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目




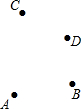 如图,已知平面内有A、B、C、D四点,按下列语句画图.
如图,已知平面内有A、B、C、D四点,按下列语句画图. 如图,CF⊥AB于点F,BE⊥AC于点E,且CF,BE交于点D,BD=CD.求证:AD平分∠BAC.
如图,CF⊥AB于点F,BE⊥AC于点E,且CF,BE交于点D,BD=CD.求证:AD平分∠BAC. 如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是D点.
如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是D点.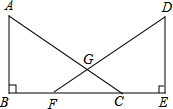 如图所示,点B、F、C、E在同一直线上,AB⊥BE、DE⊥BE.连接AC、DF,且AC=DF,AB=DE,求证:BF=CE.
如图所示,点B、F、C、E在同一直线上,AB⊥BE、DE⊥BE.连接AC、DF,且AC=DF,AB=DE,求证:BF=CE.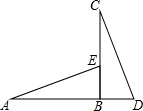 如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.判断AE与CD的数量关系和位置关系,并说明理由.
如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.判断AE与CD的数量关系和位置关系,并说明理由.