题目内容
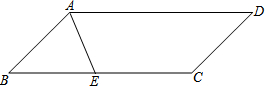 如图,在?ABCD中,AE平分∠BAD交BC于点E,
如图,在?ABCD中,AE平分∠BAD交BC于点E,(1)作CF平分∠BCD交AD于点F(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求证:△ABE≌△CDF.
考点:平行四边形的性质,全等三角形的判定,作图—基本作图
专题:
分析:(1)以点C为圆心,任意长为半径画弧,交AF,BC于两点,分别以这两点为圆心,大于这两点的距离为半径画弧,在△ABC内交于一点O,作射线BO,交AD于点F即可;
(2)根据ASA即可证明:△ABE≌△CDF.
(2)根据ASA即可证明:△ABE≌△CDF.
解答:解:(1)如图所示:
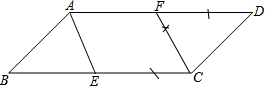
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,∠BAD=∠BCD,
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠DCF,
在△ABE和△CDF中
,
∴△ABE≌△CDF.

(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,∠BAD=∠BCD,
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠DCF,
在△ABE和△CDF中
|
∴△ABE≌△CDF.
点评:本题考查了平行四边形的性质、全等三角形的判定和性质、三角形的角平分线的画法以及角平分线的性质以及平行线的性质等知识,利用角平分线的性质得出解题关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图:若二次函数y=ax2-4x+a2-4(a为常数)的图象过(0,0),则a的值为( )
如图:若二次函数y=ax2-4x+a2-4(a为常数)的图象过(0,0),则a的值为( )| A、-2 | B、4 | C、2 | D、±2 |
 如图,PA、PB切⊙O于点A、B,PA=6,∠APB=60°,求阴影部分周长和面积.
如图,PA、PB切⊙O于点A、B,PA=6,∠APB=60°,求阴影部分周长和面积.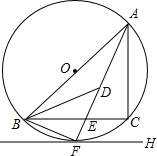 如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.