题目内容
某商场计划用66万元,购进210台冰箱和150、台彩电,若彩电的每台进价比冰箱的每台进价少400元.
(1)求冰箱、彩电的每台进价?
(2)为了满足市场需求,商场决定用不超过90 000元的资金采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的
,该商场有哪几种进货方式?
(1)求冰箱、彩电的每台进价?
(2)为了满足市场需求,商场决定用不超过90 000元的资金采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的
| 5 |
| 6 |
考点:一元一次不等式组的应用,一元一次方程的应用
专题:
分析:(1)设冰箱的进价是每台x元,则购进彩电的进价是每台(x-400)元.等量关系:两种商品的总价是66万元;
(2)设购买冰箱y台,则购买洗衣机(50-y)台,根据总费用不超过90 000元和冰箱的数量不少于彩电数量的
建立不等式组,求出其解即可.
(2)设购买冰箱y台,则购买洗衣机(50-y)台,根据总费用不超过90 000元和冰箱的数量不少于彩电数量的
| 5 |
| 6 |
解答:解:(1)设冰箱的进价是每台x元,则购进彩电的进价是每台(x-400)元.依题意得
210x+150(x-400)=660000,
解得 x=2000,
则x-400=1600.
答:冰箱、彩电的进价分别是每台2000元、1600元;
(2)设采购冰箱y台,则采购彩电(50-y)台,
由题意得
,
解得 22
≤x≤25.
∵x是正整数,
∴x的值是23,24或25.
∴该商场有三种进货方案.
方案一:采购冰箱23台,彩电27台;
方案二:采购冰箱24台,彩电26台;
方案三:采购冰箱25台,彩电25台.
210x+150(x-400)=660000,
解得 x=2000,
则x-400=1600.
答:冰箱、彩电的进价分别是每台2000元、1600元;
(2)设采购冰箱y台,则采购彩电(50-y)台,
由题意得
|
解得 22
| 8 |
| 11 |
∵x是正整数,
∴x的值是23,24或25.
∴该商场有三种进货方案.
方案一:采购冰箱23台,彩电27台;
方案二:采购冰箱24台,彩电26台;
方案三:采购冰箱25台,彩电25台.
点评:本题考查了一元一次不等式组、一元一次方程的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量(或不等)关系.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.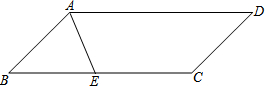 如图,在?ABCD中,AE平分∠BAD交BC于点E,
如图,在?ABCD中,AE平分∠BAD交BC于点E, 如图,在△ABC中,AB=BC=AC=BF,∠BAC=∠ABC=∠ACB,BD=DA,∠1=∠2,求∠BFD的度数.
如图,在△ABC中,AB=BC=AC=BF,∠BAC=∠ABC=∠ACB,BD=DA,∠1=∠2,求∠BFD的度数.