��Ŀ����
10����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0��4����������y=x2-4x+4�Ķ���ΪE����C������Ϊ��0��m����m��4������C����AB�ĶԳƵ��ǵ�D������BD��CD��CE��DE��1������C���߶�OB��ʱ����֤����BCD�ǵ���ֱ�������Σ�
��2����m��0ʱ������CDEΪֱ�������Σ���tan��CEO��ֵ��
��3�����P�Ǹ���������һ�㣬�Ƿ����m��ֵ��ʹ��P��C��D��EΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����������������m��ֵ���������ڣ���˵�����ɣ�

���� ��1����A��4��0����B��0��4�����ó�OB=OA=4����OBA=45�㣬��Ϊ��D���C����ֱ��AB�Գƣ�����֤�ý��ۣ�
��2����������ߵĶ��㣬����������ֱ����ۣ����ݵ���ֱ�������ε��������m��ֵ�������Ϳ����tan��CEO��ֵ��
��3����C�����߶�OB�Ϻ͵�C�����߶�OB���ӳ������������������ƽ���ı��εĶԱ�ƽ���������⼴�ɣ�
��� ��1��֤������A��4��0��B��0��4����
��OB=OA=4����OBA=45�㣬
�ߵ�D���C����ֱ��AB�Գƣ����ΪM��
��DM=CM��CD��AB��M��
���BCM=45�㣬BC=BD����BDC=45��
���BCDΪ����ֱ�������Σ�
��2���⣺��y=x2-4x+4=��x-2��2
��E��2��0����
������DCE=90��ʱ����ͼ1��
�ߡ�BCD=45�㣬
���OCE=45�㣬��OCEΪ����ֱ�������Σ�
���CEO=45��
��OC=OE=2��
��m=2��
��tan��CEO=1��
������CED=90�㣬��ͼ2����DH��x���ڵ�H��
��OB=4��OC=m��
��BC=4-m��
�ɣ�1��֪BD=BC=OH=4-m��
��EH=OH-OE=2-m��
�ߡ�CEO+��OCE=90�㣬��CEO+��HED=90�㣬
���OCE=��HED��
�֡ߡ�COE=��EHD=90�㣬
��tan��OCE=tan��HED��
��$\frac{OC}{OE}=\frac{EH}{DH}$��$\frac{m}{2}=\frac{2-m}{4}��m=\frac{2}{3}$��
��tan��CEO=$\frac{1}{3}$��
������CDE=90��ʱ����ͼ3����DF��x���ڵ�F��
�ߡ�CMB=��CDE=90�㣬
��AB��DE
���DEF=��BAO=45�㣬��DFEΪ����ֱ��������
��EF=DF=OB=4��OF=DB=CB=2��
��m=OC=6��
��tan��CEO=3��
��3����C�����߶�OB��ʱ����ͼ4����DG��OA��G��PH��DG��H��
���ı���PDCE��ƽ���ı��Σ�
��PD��CE��PD=CE��
���OCE=��HDP��
�ڡ�COE�͡�DHP�У�
$\left\{\begin{array}{l}{��OCE=��HDP}\\{��COE=��DHP}\\{PD=CE}\end{array}\right.$��
���COE�ա�DHP��
��DH=OC��PH=OE��
��C��0��m����B��0��4����E��2��0����
��DH=OC=m��PH=OE=2��
��BD=BC=4-m��
��P��6-m��4-m����
����y=x2-4x+4��4-m=��6-m��2-4��6-m��+4��
���m1=3��m2=4��
��C�����߶�OB���ӳ�����ʱ����ͼ5����DG��x����G��PH��y����H��
���ı���PCDE��ƽ���ı��Σ�
��PC��DE��PC=DE��
���GDE=��HCP
�ڡ�DGE�͡�CHP�У�
$\left\{\begin{array}{l}{��GDE=��HCP}\\{��DGE=��CHP}\\{DE=PC}\end{array}\right.$��
���PCH�ա�EDG��
��CH=DG=4��PH=GE��
��DB=BC=m-4��
��GO=DB=m-4��
��GE=m-4+2=m-2=PH��HO=m-4��
��P��m-2��m-4����
����y=x2-4x+4��m-4=��m-2��2-4��m-2��+4��
���m3=4����ȥ����m4=5��
�ʴ���m��ֵ��ʹ��P��C��D��EΪ������ı���Ϊƽ���ı��Σ���ʱm��ֵΪ3��5��
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˶��κ��������ʣ���ԳƵ����ʣ�ƽ���ı��εĶԱ�ƽ������ȵ����ʣ���2��ȷ������C��λ���ǽ���Ĺؼ�����3���ѵ����ڷ�������ۣ�

| A�� | 7��7.5 | B�� | 7��8 | C�� | 9��7.5 | D�� | 7.5��7 |
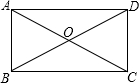 ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AB=3����AOD=120�㣬��AD�ij�Ϊ��������
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AB=3����AOD=120�㣬��AD�ij�Ϊ��������| A�� | 3 | B�� | 3$\sqrt{3}$ | C�� | 6 | D�� | 3$\sqrt{5}$ |

| A�� | 240��cm2 | B�� | 480��cm2 | C�� | 1200��cm2 | D�� | 2400��cm2 |
 ��ͼ���ֱ������������y=$\frac{3}{x}$ͼ���ϵĵ�P1��1��y1����P2��2��y2��������Pn��n��yn��������x��Ĵ��ߣ�����ֱ�ΪA1��A2��A3��An������A1P2��A2P3������An-1Pn��������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3�����˴����ƣ����B10����������$\frac{63}{110}$��
��ͼ���ֱ������������y=$\frac{3}{x}$ͼ���ϵĵ�P1��1��y1����P2��2��y2��������Pn��n��yn��������x��Ĵ��ߣ�����ֱ�ΪA1��A2��A3��An������A1P2��A2P3������An-1Pn��������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3�����˴����ƣ����B10����������$\frac{63}{110}$�� �ڡ�ABC�У���ACB=90�㣬AC=BC=2��M�DZ�AC���е㣬CH��BM��H��
�ڡ�ABC�У���ACB=90�㣬AC=BC=2��M�DZ�AC���е㣬CH��BM��H��
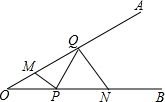 ��ͼ����AOB=30�㣬��M��N�ֱ��ڱ�OA��OB�ϣ���OM=1��ON=3����P��Q�ֱ��ڱ�OB��OA�ϣ���MP+PQ+QN����Сֵ��$\sqrt{10}$��
��ͼ����AOB=30�㣬��M��N�ֱ��ڱ�OA��OB�ϣ���OM=1��ON=3����P��Q�ֱ��ڱ�OB��OA�ϣ���MP+PQ+QN����Сֵ��$\sqrt{10}$��