题目内容
18.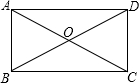 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{5}$ |
分析 先由矩形的性质得出∠BAD=90°,OA=OB,再证明△AOB是等边三角形,得出OB=AB=3,BD=6,然后由勾股定理求出AD即可.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=3,
∴BD=2OB=6,
∴AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
故选:B.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
8.甲、乙两名队员在5次设计测试中,命中环数的平均数都是8环,各次成绩分别如下: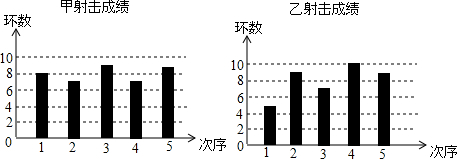
以下关于甲乙射击成绩的比较,正确的是( )

以下关于甲乙射击成绩的比较,正确的是( )
| A. | 甲的中位数较大,方差较小 | B. | 甲的中位数较小,方差较大 | ||
| C. | 甲的中位数和方差都比乙小 | D. | 甲的中位数和方差都比乙大 |
9. 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )| A. | 2π | B. | 3π | C. | 4π | D. | 6π |
 如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,试求证:∠BDC=90°-$\frac{1}{2}$∠A.
如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,试求证:∠BDC=90°-$\frac{1}{2}$∠A.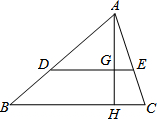 如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.
如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.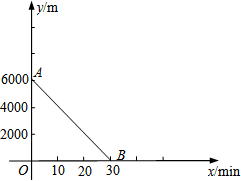 某日,小敏、小君两人约好去奥体中心打球.小敏13:00从家出发,匀速骑自行车前往奥体中心,小君13:05从离奥体中心6000m的家中匀速骑自行车出发.已知小君骑车的速度是小敏骑车速度的1.5倍.设小敏出发x min后,到达离奥体中心y m的地方,图中线段AB表示y与x之间的函数关系.
某日,小敏、小君两人约好去奥体中心打球.小敏13:00从家出发,匀速骑自行车前往奥体中心,小君13:05从离奥体中心6000m的家中匀速骑自行车出发.已知小君骑车的速度是小敏骑车速度的1.5倍.设小敏出发x min后,到达离奥体中心y m的地方,图中线段AB表示y与x之间的函数关系.

 如图是一个点阵,从上往下有无数多行,其中第一行有2个点,第二行有5个点,第三行有11个点,第四行有23个点,…,按此规律,第n行有3•2n-1-1个点.
如图是一个点阵,从上往下有无数多行,其中第一行有2个点,第二行有5个点,第三行有11个点,第四行有23个点,…,按此规律,第n行有3•2n-1-1个点.