题目内容
1. 如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn),…作x轴的垂线,垂足分别为A1、A2、A3…An…连接A1P2,A2P3,…,An-1Pn,…再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,…此次类推,则点B10的纵坐标是$\frac{63}{110}$.
如图,分别过反比例函数y=$\frac{3}{x}$图象上的点P1(1,y1),P2(2,y2),…,Pn(n,yn),…作x轴的垂线,垂足分别为A1、A2、A3…An…连接A1P2,A2P3,…,An-1Pn,…再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,…此次类推,则点B10的纵坐标是$\frac{63}{110}$.
分析 根据反比例函数图象上点的坐标特征求得点P1、P2的纵坐标,由平行四边形对边平行且相等的性质求得点B1的纵坐标是y2+y1、B2的纵坐标是y3+y2、B3的纵坐标是y4+y3,据此可以推知点Bn的纵坐标是:yn+1+yn=$\frac{3}{n+1}+\frac{3}{n}$=$\frac{6n+3}{n(n+1)}$,把n=10代入即可.
解答 解:∵点P1(1,y1),P2(2,y2)在反比例函数y=$\frac{3}{x}$的图象上,
∴y1=3,y2=$\frac{3}{2}$,
∴P1A1=y1=3;
又∵四边形A1P1B1P2,是平行四边形,
∴P1A1=B1P2=3,P1A1∥B1P2 ,
∴点B1的纵坐标是:y2+y1=$\frac{3}{2}$+3,即点B1的纵坐标是$\frac{9}{2}$,
同理求得,点B2的纵坐标是:y3+y2=1+$\frac{3}{2}$=$\frac{5}{2}$,
点B3的纵坐标是:y4+y3=$\frac{3}{4}$+1=$\frac{7}{4}$,
…
点Bn的纵坐标是:yn+1+yn=$\frac{3}{n+1}+\frac{3}{n}$=$\frac{6n+3}{n(n+1)}$,
当n=10时,$\frac{6×10+3}{10×(10+1)}$=$\frac{63}{110}$,
故答案是:$\frac{63}{110}$.
点评 本题考查了平行四边形的性质、反比例函数图象上点的坐标特征、反比例函数的图象.解答此题的关键是根据平行四边形的对边平行且相等的性质求得点Bn的纵坐标yn+1+yn.

练习册系列答案
相关题目
9. 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为( )| A. | 2π | B. | 3π | C. | 4π | D. | 6π |
11.下列命题中是真命题的是( )
| A. | 若a>b,则ac2>bc2 | |
| B. | 对角线互相垂直且相等的四边形是正方形 | |
| C. | 两个等腰直角三角形一定相似 | |
| D. | 打开数学课本,恰好翻到第88页是必然事件 |
 已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.
已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.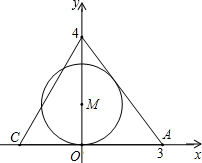 如图,直角坐标系中,点A(3,0)、B(0,4)分别位于x轴和y轴上,点C在x轴的负半轴上,且∠ACB=60°,在y轴正半轴上有一点M,以M为圆心,MO为半径作⊙M与BA相切,若保持圆的大小不变,△ABC位置不变,将⊙M向右平移$\frac{\sqrt{3}}{6}$个单位,⊙M与BC相切.
如图,直角坐标系中,点A(3,0)、B(0,4)分别位于x轴和y轴上,点C在x轴的负半轴上,且∠ACB=60°,在y轴正半轴上有一点M,以M为圆心,MO为半径作⊙M与BA相切,若保持圆的大小不变,△ABC位置不变,将⊙M向右平移$\frac{\sqrt{3}}{6}$个单位,⊙M与BC相切.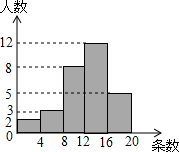 某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.
某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数. 如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,试求证:∠BDC=90°-$\frac{1}{2}$∠A.
如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,试求证:∠BDC=90°-$\frac{1}{2}$∠A.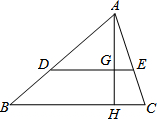 如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.
如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.