题目内容
5. 在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.
在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.(1)试求sin∠MCH的值;
(2)求证:∠ABM=∠CAH.
分析 (1)由勾股定理求出MB,证出∠MCH=∠MBC,得出sin∠MCH=sin∠MBC,即可得出结果;
(2)先由射影定理得出AM2=MC2=MH•MB,得出比例式$\frac{MA}{MH}=\frac{MB}{MA}$,证出△AMH∽△BMA,得出对应角相等即可.
解答 (1)解:在△MBC中,∠MCB=90°,BC=2,
又∵M是边AC的中点,
∴AM=MC=$\frac{1}{2}$BC=1,
∴MB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵CH⊥BM于H,
∴∠MHC=90°,
∴∠MCH+∠BMC=90°,
∵∠MBC+∠BMC=90°,
∴∠MCH=∠MBC,
∴sin∠MCH=sin∠MBC=$\frac{MC}{MB}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$;
(2)证明:∵∠ACB=90°,CH⊥BM,
根据射影定理得:AM2=MC2=MH•MB,
∴$\frac{MA}{MH}=\frac{MB}{MA}$,
又∵∠AMH=∠BMA,
∴△AMH∽△BMA,
∴∠ABM=∠CAH.
点评 本题考查了相似三角形的判定与性质、勾股定理、解直角三角形;熟练掌握相似三角形的判定与性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
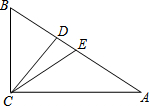 在直角三角形ABC中,CD、CE分别是斜边AB上的高、中线,BC=a,AC=b
在直角三角形ABC中,CD、CE分别是斜边AB上的高、中线,BC=a,AC=b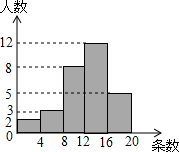 某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.
某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.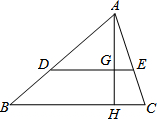 如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.
如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$. 如图,AB∥DE,∠1=∠2.求证:AE∥DC.
如图,AB∥DE,∠1=∠2.求证:AE∥DC.
 如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).