题目内容
20.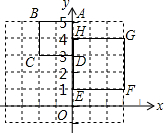 如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是(0,$\frac{17}{5}$),(-6,7).
如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是(0,$\frac{17}{5}$),(-6,7).
分析 分别利用待定系数法求出一次函数解析式,再利用当B与F是对应点,以及当D与F是对应点分别求出位似中心.
解答 解:设当B与F是对应点,设直线BF的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=5}\\{3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{5}}\\{b=\frac{17}{5}}\end{array}\right.$,
故直线BF的解析式为:y=-$\frac{4}{5}$x+$\frac{17}{5}$,
则x=0时,y=$\frac{17}{5}$,
即位似中心是:(0,$\frac{17}{5}$),
设当C与E是对应点,设直线CE的解析式为:y=ax+c,
则$\left\{\begin{array}{l}{-2a+c=3}\\{c=1}\end{array}\right.$,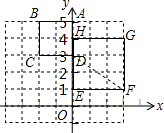
解得:$\left\{\begin{array}{l}{a=-1}\\{c=1}\end{array}\right.$,
故直线CE的解析式为:y=-x+1,
设直线DF的解析式为:y=dx+e,
则$\left\{\begin{array}{l}{3d+e=1}\\{e=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{d=-\frac{2}{3}}\\{e=3}\end{array}\right.$,
故直线DF的解析式为:y=-$\frac{2}{3}$x+3,
则$\left\{\begin{array}{l}{y=-\frac{2}{3}x+3}\\{y=-x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-6}\\{y=7}\end{array}\right.$
即位似中心是:(-6,7),
综上所述:所述位似中心为:(0,$\frac{17}{5}$),(-6,7).
故答案为:(0,$\frac{17}{5}$),(-6,7).
点评 此题主要考查了位似图形的性质以及待定系数法求一次函数解析式,正确分类讨论得出是解题关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形 的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )
的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )| A. | Sn=3×22n+1 | B. | Sn=3×22n+3 | C. | Sn=3×22n-3 | D. | Sn=3×22n |
| A. | -15 | B. | 15 | C. | 2 | D. | -8 |
| A. | 开口向下 | B. | 对称轴是x=-2 | C. | 顶点坐标是(2,3) | D. | 与x轴有两个交点 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,$\widehat{BC}=\widehat{PC}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,$\widehat{BC}=\widehat{PC}$.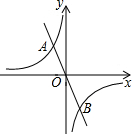 如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A,B,若点A的坐标为(-2,3),则点B的坐标为(2,-3).
如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A,B,若点A的坐标为(-2,3),则点B的坐标为(2,-3).