题目内容
多项式（x+y-z）（x-y+z）-（y+z-x）（z-x-y）的公因式是（ ）
| A、x+y-z | B、x-y+z |
| C、y+z-x | D、不存在 |
考点：公因式
专题：
分析：根据原式，将（z-x-y）提取负号，进而得出公因式即可．
解答：解：（x+y-z）（x-y+z）-（y+z-x）（z-x-y）
=（x+y-z）（x-y+z）+（y+z-x）（x+y-z）
=（x+y-z）（x-y+z+y+z-x）
=2z（x+y-z），
故多项式（x+y-z）（x-y+z）-（y+z-x）（z-x-y）的公因式是：x+y-z．
故选：A．
=（x+y-z）（x-y+z）+（y+z-x）（x+y-z）
=（x+y-z）（x-y+z+y+z-x）
=2z（x+y-z），
故多项式（x+y-z）（x-y+z）-（y+z-x）（z-x-y）的公因式是：x+y-z．
故选：A．
点评：此题主要考查了公因式的定义，正确找出公因式是解题关键．
练习册系列答案
相关题目
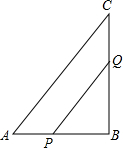如图，在△ABC中，AB=6cm，BC=8cm，∠B=90°，点P从点A开始沿边AB向点B以1cm每秒的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm每秒的速度移动．如果P、Q分别从A、B同时出发，经过几秒，△BPQ的面积等于8cm2？
如图所示，在矩形ABCD中，两条对角线AC、BD相交于点O，∠AOB=60°，AB=6．
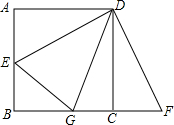如图，已知正方形ABCD的边长为8，E为AB上一点，点B、C、F在同一条直线上，且AE=CF，当∠EDG为多少度时，存在AE+CG=EG，并证明这个结论．
如图，△ABC与△BDE均为等腰直角三角形，BA⊥AC，DE⊥BD，点D在AB边上，连结EC，取EC中点F，求证：