题目内容
2.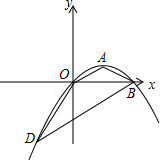 已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0).
已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0).(1)当s=2时,t=1时,求抛物线对应的二次函数的表达式;
(2)若(1)中的抛物线与x轴交于点B,过B作OA的平行线交抛物线于点D,求△BDO三条高的和;
(3)当点A在抛物线y=x2-x上,且-1≤s<2时,求a的取值范围.
分析 (1)由题意可知A(2,1),设抛物线的解析式为y=a(x-2)2+1,由于抛物线过原点,所以将(0,0)代入即可求出a的值.
(2)根据A(2,1)可求出OA的直线解析式,由于DB∥OA,所以一次项系数必定相等,从而可求出直线BD的解析式,联立直线BD与抛物线的解析式即可求出D的坐标,然后根据勾股定理分别求出OD、BD的长度,再求出△BOD的面积即可求出△BDO三条高的和.
(3)t=s2-s,由于A(s,t)是y=ax2+bx+c(a≠0)的顶点,所以y=a(x-s)2+t,将(0,0)代入该式后可得s=(a+1)s2,利用s的范围即可求出a的范围.
解答 解:(1)由题意可知A(2,1),
设抛物线的解析式为y=a(x-2)2+1,
由于抛物线过原点,
∴将(0,0)代入y=a(x-2)2+1,
∴解得a=-$\frac{1}{4}$,
∴抛物线的解析式为:y=-$\frac{1}{4}$(x-2)2+1,
(2)令y=0代入y=-$\frac{1}{4}$(x-2)2+1,
∴解得x=4或x=0,
∴B(4,0)
设直线OA的解析式为:y=kx,
将A(2,1)代入y=kx,
∴k=$\frac{1}{2}$,
∵BD∥OA,
∴设直线BD的解析式为:y=$\frac{1}{2}$x+m,
将B(4,0)代入y=$\frac{1}{2}$x+m,
∴m=-2
∴直线BD的解析式为:y=$\frac{1}{2}$x-2
联立$\left\{\begin{array}{l}{y=\frac{1}{2}x-2}\\{y=-\frac{1}{4}(x-2)^{2}+1}\end{array}\right.$
解得:x=4或x=-2
∴D(-2,-3)
∴由勾股定理可知:OD=$\sqrt{13}$,BD=3$\sqrt{5}$,
设OB、OD、BD边上的高分别为h1,h2,h3,
∴h1=3
又∵OB=4,
∴S△BDO=$\frac{1}{2}$OB•h1=6,
∴$\frac{1}{2}$BD•h3=$\frac{1}{2}$OD•h2=6,
∴h2=$\frac{12\sqrt{13}}{13}$,h3=$\frac{4\sqrt{5}}{5}$,
∴△BDO三条高的和h1+h2+h3=3+$\frac{12\sqrt{13}}{13}$+$\frac{4\sqrt{5}}{5}$,
(3)由题意可知:t=s2-s,
∵A(s,t)是y=ax2+bx+c(a≠0)的顶点,
∴y=a(x-s)2+t,
又因为该抛物线经过原点,
∴0=as2+t,
∴0=as2+s2-s,
∴s=(a+1)s2,
当s=0时,
此时,a全体实数,
当s≠0时,此时-1≤s<0或0<s<2,
∴a=$\frac{1}{s}-1$,
∴a≤-2或a>-$\frac{1}{2}$,
综上所述,a≤-2或a>-$\frac{1}{2}$,
点评 本题考查二次函数的综合问题,解题的关键是熟练运用二次函数的性质,综合运用了待定系数法,解方程组等知识,综合程度较高,本题属于难题.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案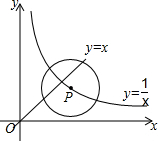 如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )| A. | 1≤x≤$\sqrt{2}$ | B. | $\sqrt{2}-1≤x≤\sqrt{2}$ | C. | $\sqrt{2}-1≤x≤1$ | D. | $\sqrt{2}-1≤x≤\sqrt{2}+1$ |
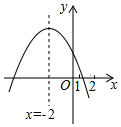 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 人数 | 3 | 4 | 8 | 12 | 3 |
| 成绩(次/分钟) | 121 | 157 | 176 | 178 | 184 |
| A. | 175 | B. | 176 | C. | 177 | D. | 178 |
| A. | x2•x3=x6 | B. | (x3)2=x5 | C. | (-2x2y)3=-8 x6y3 | D. | -x+2x=-3x |

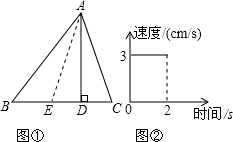 如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②
如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图② 如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.
如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.