题目内容
15.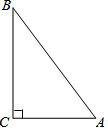 已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.
已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.
分析 设A′B′交AC于F.在Rt△ABC中,求出AC、BC,在Rt△A′CB′中,求出AF、A′F,利用EF∥CB,推出$\frac{EF}{BC}$=$\frac{AF}{AC}$,求出EF即可解决问题.
解答 解:设A′B′交AC于F.
∵△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$,
∴AC=6,BC=8,
∵CF⊥A′B′,
∴CF=$\frac{6×8}{10}$=$\frac{24}{5}$,AF=6-$\frac{24}{5}$=$\frac{6}{5}$,
A′F=$\sqrt{A′{C}^{2}-C{F}^{2}}$=$\frac{18}{5}$,
∵EF∥CB,
∴$\frac{EF}{BC}$=$\frac{AF}{AC}$,
∴$\frac{EF}{8}$=$\frac{\frac{6}{5}}{6}$,
∴EF=$\frac{8}{5}$,
∴B′E=10-$\frac{18}{5}$-$\frac{8}{5}$=$\frac{24}{5}$.
故答案为$\frac{24}{5}$.
点评 本题考查旋转变换、解直角三角形.平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
7.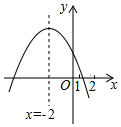 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
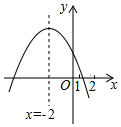 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,下列结论:①abc<0;②4a+b=0;③9a-3b+c<0;④3a+c>0,其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.若二次函数y=x2-2x+c的图象与x轴没有交点,则c的值可能是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
 如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.
如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.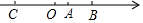 如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.
如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.