题目内容
8. 如图,已知△ABC中∠A=43°,∠B=73°,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=16度.
如图,已知△ABC中∠A=43°,∠B=73°,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=16度.
分析 首先利用三角形内角和定理可求出∠ACB=64°,然后利用等边对等角和三角形的外角性质可求得∠CGD=∠CDG=32°,同样的方法可求出∠E的度数.
解答 解:∵∠A=43°,∠B=73°,
∴∠ACB=180°-∠A-∠B=64°,
∵CF=CD,
∴∠CGD=∠CDG,
又∵∠ACB=∠CGD+∠CDG,
∴∠CGD=∠CDG=32°,
∵DF=DE,
∴∠DFE=∠E,
又∵∠CDG=∠DFE+∠E,
∴∠DFE=∠E=16°,
故答案为:16.
点评 本题考查了三角形内角和定理,三角形的外角性质和等腰三角形的性质,解答本题的关键是正确识图并熟练掌握相关的各个定理与性质.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
19.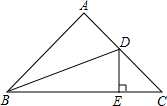 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,交AC于点D,DE⊥BC,若BC=10cm,则△DEC的周长为( )
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,交AC于点D,DE⊥BC,若BC=10cm,则△DEC的周长为( )
 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,交AC于点D,DE⊥BC,若BC=10cm,则△DEC的周长为( )
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,交AC于点D,DE⊥BC,若BC=10cm,则△DEC的周长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 14cm |
18.下列运算正确的是( )
| A. | 3x-2x=1 | B. | -2x-2=-$\frac{1}{2{x}^{2}}$ | C. | (-a)2•a3=a6 | D. | (-a2)3=-a6 |
 如图是一个正方形的展开图,每个面上都注明了字母,知道字母E的对面是D.
如图是一个正方形的展开图,每个面上都注明了字母,知道字母E的对面是D. 如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=4,求点B的坐标.
如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=4,求点B的坐标. 如图,∠AOC和∠BOD都是直角,如果∠AOB=150°,那么∠COD=30度.
如图,∠AOC和∠BOD都是直角,如果∠AOB=150°,那么∠COD=30度.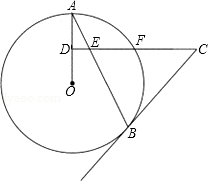 如图,已知点A,B在⊙O上,AO是⊙O的半径,D为AO的中点,过点D作CD⊥AO于点D,连接AB交CD于点E,且CE=CB.
如图,已知点A,B在⊙O上,AO是⊙O的半径,D为AO的中点,过点D作CD⊥AO于点D,连接AB交CD于点E,且CE=CB.