题目内容
3. 如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=4,求点B的坐标.
如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=4,求点B的坐标.
分析 过点B作BE⊥OE于E,有OC=4,边OA与x轴正半轴的夹角为30°,可求出AC的长,根据矩形的性质可得OB的长,进而求出BE,OE的长,从而求出点B的坐标.
解答 解:过点B作BE⊥OE于E,
∵矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,
∴∠CAO=30°,
∴AC=8,
∴OB=AC=8,
由矩形的性质可知∠BOA=∠CAO=30°,
∴∠OBE=180°-30°-30°-90°=30°,
∴OE=4,
∴BE=4$\sqrt{3}$,
∴则点B的坐标是(4,4$\sqrt{3}$).
点评 本题考查了矩形的性质,直角三角形的性质以及勾股定理的运用和解直角三角形的有关知识,解题的关键是作高线得到点的坐标的绝对值的长度,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.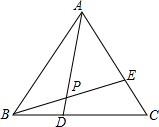 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
14. 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 65° |
11. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
18. 如图,两个三角形关于某直线对称,则x=( )°.
如图,两个三角形关于某直线对称,则x=( )°.
 如图,两个三角形关于某直线对称,则x=( )°.
如图,两个三角形关于某直线对称,则x=( )°.| A. | 34 | B. | 35 | C. | 36 | D. | 37 |
15.下列函数中,一次函数有( )
| A. | y=-8x | B. | y=$\frac{-8}{x}$ | C. | y=-8x2+6 | D. | y=-0.5x-1 |
12.下列运算中正确的是( )
| A. | a+a=a2 | B. | a•a2=a2 | C. | (ab)2=a2b2 | D. | (a2)3=a5 |
 如图,已知△ABC中∠A=43°,∠B=73°,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=16度.
如图,已知△ABC中∠A=43°,∠B=73°,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=16度.