题目内容
9.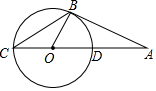 如图,AB是⊙O的切线,点C在⊙O上,且AC经过点O,若∠A=20°,AD=2,AB=4.
如图,AB是⊙O的切线,点C在⊙O上,且AC经过点O,若∠A=20°,AD=2,AB=4.(1)求∠C的度数;
(2)求⊙O的半径.
分析 (1)利用切线的性质得∠ABO=90°,则利用互余可计算出∠AOB=70°,然后根据三角形外角性质和等腰三角形的性质可计算出∠C的度数;
(2)设⊙O的半径为r,在Rt△AOB中利用勾股定理得到r2+42=(r+2)2,然后解方程求出r即可.
解答 解:(1)∵AB是⊙O的切线,
∴OB⊥AB,
∴∠ABO=90°,
∴∠AOB=90°-∠A=90°-20°=70°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC,
∴∠C=$\frac{1}{2}∠$AOB=35°;
(2)设⊙O的半径为r,则OB=OD=r,
在Rt△AOB中,∵OB2+AB2=AO2,
∴r2+42=(r+2)2,解得r=3,
即⊙O的半径为3.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
17.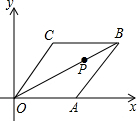 已知菱形OABC在平面直角坐标系中的位置如图所示,顶点A在x轴的正半轴上,OB=4$\sqrt{3}$,∠COA═60°,点P是对角线OB上的一个动点,点D的坐标为(0,1),则CP+DP的最小值为( )
已知菱形OABC在平面直角坐标系中的位置如图所示,顶点A在x轴的正半轴上,OB=4$\sqrt{3}$,∠COA═60°,点P是对角线OB上的一个动点,点D的坐标为(0,1),则CP+DP的最小值为( )
 已知菱形OABC在平面直角坐标系中的位置如图所示,顶点A在x轴的正半轴上,OB=4$\sqrt{3}$,∠COA═60°,点P是对角线OB上的一个动点,点D的坐标为(0,1),则CP+DP的最小值为( )
已知菱形OABC在平面直角坐标系中的位置如图所示,顶点A在x轴的正半轴上,OB=4$\sqrt{3}$,∠COA═60°,点P是对角线OB上的一个动点,点D的坐标为(0,1),则CP+DP的最小值为( )| A. | 5 | B. | $\sqrt{17}$ | C. | 4 | D. | $\sqrt{3}$ |
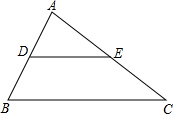 如图,在△ABC中,DE∥BC,且S△ADE:S四边形BCED=1:2,BC=26,求DE的长.
如图,在△ABC中,DE∥BC,且S△ADE:S四边形BCED=1:2,BC=26,求DE的长. 如图,长方形ABCD的面积为8,点C的坐标为(0,1),点D的坐标为(0,3),则点A的坐标为(-4,3),点B的坐标为(-4,1).
如图,长方形ABCD的面积为8,点C的坐标为(0,1),点D的坐标为(0,3),则点A的坐标为(-4,3),点B的坐标为(-4,1).