题目内容
10.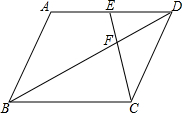 如图,在?ABCD中,F是对角线BD上的一点,连接CF并延长交AD于点E.若$\frac{BF}{DF}$=$\frac{1}{n}$,则$\frac{EF}{EC}$=n:(n+1).
如图,在?ABCD中,F是对角线BD上的一点,连接CF并延长交AD于点E.若$\frac{BF}{DF}$=$\frac{1}{n}$,则$\frac{EF}{EC}$=n:(n+1).
分析 根据平行四边形的性质得到AD∥BC,证得△DEF∽△BCF,根据相似三角形的性质得到$\frac{BF}{DF}=\frac{CF}{EF}$,于是得到$\frac{BF}{DF}=\frac{CF}{EF}$=$\frac{1}{n}$,即可得到结论.
解答 解:∵在?ABCD中,
∴AD∥BC,
∴△DEF∽△BCF,
∴$\frac{BF}{DF}=\frac{CF}{EF}$,
∵$\frac{BF}{DF}$=$\frac{1}{n}$,
∴$\frac{BF}{DF}=\frac{CF}{EF}$=$\frac{1}{n}$,
∴$\frac{EF}{EC}$=n:(n+1).
故答案为:n:(n+1).
点评 此题主要考查了相似三角形的判定与性质,根据已知得出△DEF∽△BCF是解题关键.

练习册系列答案
相关题目
15.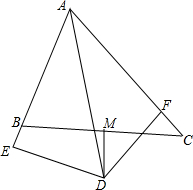 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;其中正确的有( )
 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列命题是真命题的是( )
| A. | 同位角相等 | B. | 平行于同一直线的两条直线平行 | ||
| C. | 点(2,3)在直线y=2x+3上 | D. | 函数y=-x+1中y随x的增大而增大 |
 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为10cm.
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为10cm. 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切. 用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.
用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.